수업후기

#0
지난 시간 한 것 복습하면, 대칭 4가지 중 첫 번째 space-time이다. 공간이동에 대해서 변하지 않는 것, 공간대칭이고 운동량 상수이다. 시간에 대한 대칭은 에너지이다. 시공간은 spacetime으로 translation은 이동시켰다는 것으로, 공간에 대해서도 시간에 대해서도 이동시킨 것이다. 물리학은 아름다움을 추구한다는 말이 여러 군데 있다. 인간이 잡다하게 생각하는 것을 모아주기에 아름답다. 이동을 공간에 대해서만 쓰는데, 시간에 대해서도 구분하지 않고 한꺼번에 쓴다는 것이 물리학 정신이다. 그래서 우주의 대부분을 알게 되었다. 시간공간 구분하지 말고 한 덩어리로 보고 시간대칭, 공간대칭을 본다.
두 번째 permutation도 대칭이다. 자리 바꾸는 것이 치환, 재배치이다. 그것이 로벨리 버전으로는 “우리는 원자로 되어 있는 것이 아니고 원자의 배열로 되어 있다.”는 것이다. 배열이 엔트로피이다. 에너지보다 더 위의 개념이 배치라는 개념의 엔트로피이다. 우리가 하는 효율성은 에너지는 사라지지 않지만 효율성 높은 에너지와 낮은 에너지가 있다. 애들이 떠드는 에너지는 시끄럽고 효율이 없다. 관현악단의 에너지는 정서적 공간의 효율이 다르다. 에너지는 불변이라는 말은 에너지는 변하지만 총량이 안 변한다는 것이다. 항상 바뀔 때 ‘좋은 에너지’, ‘나쁜 에너지’가 있는데, 늙어 죽어가는 것은 나쁜 에너지가 많아지는 것이다. 즉 가지런한 배열이 사라지는 것이다. 에너지 보다 더 위의 개념이 엔트로피이고, 엔트로피가 배열이다. 배열이 바뀐다는 것은 총에너지는 안 바뀌지만 자리를 바꿀 수 있다. 배열만 바뀐 것이다. 그러면 색깔이 달라지고 모든 것이 달라진다. 물리학은 가지런해지는 세계를 훈련하기에 명상보다 더 빠를 수 있다. 모두 대칭을 얘기한다. 우주를 설명하는 페르미온과 보손의 2가지 입자의 명쾌한 설명이 permutation에서 나온다. 대칭에도 대칭과 반대칭이 있다. 반대칭은 부호만 바뀐 것으로 페르미온이다. 알려고 하지 말고 암기하라. 수학적으로는 기함수냐 우함수냐이다.
공부는 지금 단계에서 아는 것에서 매듭을 지어주어야 한다. 70%에서 만족하고 더 이상 가려고 하지 말고 보자기에 싸 두어야 한다. 그래야 정신이 안 사나워진다. 안 좋은 에너지가 많아지면 풀어지고 그 분야가 재미없어진다. 내가 요까지 안 것을 정확하게 선을 긋고 거기까지는 내가 에너지 안 쓰고도 인출할 수 있고, 다음에는 거기서부터 다시 시작한다. 금방 올라간다. 그렇게 하지 않고 모르는 것 알아야 한다고 에너지 쓰다가는 퍼져 버린다.
다음은 internal symmetry, 그리고 Gauge symmetry 놀랍다. 놀라워해야 하는 것은 이렇게 4개로 구분할 수 있고 여기서 빠져나갈 것이 거의 없다는 것이고, 이런 것을 완결된 지식이라고 한다. 연구자는 완결된 지식을 추구하면 안 된다. 논문을 써야 하기에 새로운, 가려운 데를 끝까지 물고 늘어져야 한다. 여러분은 연구원이 아니다. 우라나라 과학교육이 잘못 된 것이 연구자를 표상으로 하는 것을 모든 사람들에게 하라는 것이다. 우리는 과학자가 되려는 것이 아니고 과학적 사고를 배우는 것이다. 그러면 연구자들의 결과를 얼마나 짧은 시간에 핵심을 내 것으로 만드느냐이다. 우리는 새로운 것을 발견하는 것이 아니다. 원초적으로 할 수가 없다. 창의성은 초등학생용이 아니고, 전문가용이다. 엉뚱한 헛발질 하지 마라. 새로운 과학지식을 만들어낼 수 없다. 그렇게 하지 않아도 된다.
우리가 연구자가 아님을 항상 잊으면 안 된다. 제발 환상을 갖지 마라. 연구자는 직업상으로 한 분야 밖에 못하도록 규정된 사람이다. 다른 것 하면 못 버틴다. 연구자들은 궁극을 아는 것이 아니다. 노밸상 받은 디랙도 방정식을 유도하고 반물질을 아는데까지 2년 동안 헛발질 했다. 아인슈타인이 중력장방정식 유도하는 과정에 쓴 논문의 상당수가 틀린 논문이다. 우주의 궁극을 알고싶은 사람에게는 연구자를 권하지 않는다. 연구자들은 많은 것 중에 하나를 한다. 그러나 궁극은 그 하나로 해결이 안된다. 그래서 입자물리학 했다가 브레인했다가 지질학 했다가 진화학 하는 것이다. 10년 전만 해도 이렇게 하는 사람이 아웃사이더였으나 지금은 메인이 되었다. 서점에 빅히스토리류 책이 장악을 했다. 지금은 돌이킬 수 없다. AI 시대에 한 분야를 한다는 것은 거의 의미가 없을 정도이다. 한 분야에서 아무리 놀라운 것을 해도 우주전체를 알 수 없다. 효율을 따져야 한다. 이 도표는 올해 발견한 자료 중 최고이다. 대칭에 대해 잡다하게 할 필요 없다. 이 도표 하나만 암기하면 된다.
파인만다이아그램에서 모든 정보는 전달이 되었다. 이름만 붙이면 된다. 지금까지 구조를 모르는 것이다. 구조만 알면 이름만 붙이면 된다. 전체구조를 보면 W+, X-는 대칭이다. 대칭구조를 알기에 기억하기 편하다. charge를 기억하기 위해 uct, dsb로 암기하도록 하였다. dsb에서 d와 b가 대칭이 되어있다. 피식 웃을 일이 아니다. 이렇게 찾아내는데 어마어마한 시간이 걸린다. 유럽사 강의에서도 ‘루루필 루루필 루필사필 장사사 / 사루사루 프앙프사 앙앙루’ 기억나는가? 4-5년전 강의인데, 당시 반응이 반은 픽 웃었다. 픽 웃은 사람은 10년이 지나도 블란서사 들어갈 수 없다. 이거 암기하는데 시간 얼마 걸리는가? 1시간도 안 걸린다. 이 정보가 어마어마하다. 간단한 것을 기억하지 못해 결국 그 분야를 못 한다.
산책가서 뭘 했는가를 지난 몇 년간 이야기 해 주었다. 또 해주면, 이번주에 산책가서 기억한 것이 오늘 강의 주제이다. 뭘 기억했는가? “델지지지델지”이다. 상대성이론 유도하는 과정에서 하나의 포인트가 잘 안된다. 딴 얘기하다보면 풀다가 미끄러진다. 그래서 산책하면서 30분동안 “델지지지델지” 암기했다. 이것이 심어지지 않으면 중력장방정식 유도 못한다. 전체과정에서 대못처럼 박혀있는 것의 대못을 뽑아내지 않으면 자기 것이 되지 않는다. 그래서 이해하는 것이 공부가 아니다. 이해된다고 내 것이 되지 않는다. 코아가 몇 개 없다. 하루를 다 보내도 내 몸에 심겠다는 각오로 대못을 뽑아주어야 한다. 대못이 다 뽑히면 10년간 안 잊어버린다.
dsb와 usb가 스위칭 되는 것을 flavor change라고 한다. Neutral charge는 flavor change가 안된다. flavor change라는 용어가 내 몸에 붙어야 한다. quark에는 색과 향이 있다고 한다. 색이 color, 향이 flavor이다. 색은 rgb로 설명을 하는데, 향은 뭔가? 많은 자료에서 설명이 와닿지가 않는다. 입자물리학이 어려운 이유는 핵심용어가 정확히 와닿지 않아서이다. flavor change는 (u,c,t)와 (d,s,b)가 왔다갔다한다는 말이다. 또 (e, νe)와 (μ, νμ)이 왔다갔다하는 것이다. flavor change는 전하량이 바뀐다. neutral current, z0는 flavor change를 못한다. 전하량이 바뀌려면 매개해주는 입자가 전하를 띄어야 한다. 1973년 가가멜 거품상자에서 neutral charge를 발견하고 전셰계 물리학계에서 경악을 했다. “neutral current는 flavor change를 못하고 charged current만이 flavor change를 할 수 있다”를 기억하라. 핵심은 용어에 다 있다.
입자는 반드시 쌍생성 쌍소멸된다. 모든 입자는 혼자 안 생긴다. charge conservation 때문이다. 자연과학에서 한번도 깨진 바 없는 절대법칙이다. 그것의 다른 말이 쌍생성이다. 물질과 반물질이 쌍으로 생긴다. 전자와 양전자가 충돌하여 쌍소멸하면 광자로 바뀐다. 이때 광자는 자기 자신이 반광자가 된다.
Quark이 섞일 수 있는데, u와 d는 90%, u와 s는 10% 섞이는데, 이것을 cosΘ+isinΘ로 표시할 수 있다. 각도가 1-10도면, cos은 1에, sin은 0에 가까운 것을 쓴다. 이것을 확장해서 만든 테이블이 CKM 매트릭스이다. 먼저 용어만 박아 놓으라.
Tensor product(⊗), direct sum(⊕)은 group theory를 모르고는 들어갈 수 없다. direct sum(⊕)은 그룹을 어떻게 나눌 것인가이다. 이름만 알아두어라. 집합론 연산기호이다.
파인만 다이아그램이다. 모든 소립자의 상호작용은 이 그림의 수식으로 표현이 된다. 이름만 먼저 알아라. 내용은 나중에 해도 된다. 입자끼리 충돌의 모든 확률을 계산할 수 있다. 이쪽 전공자는 매일 이것을 계산한다. 모멘텀이 모든 것을 갖고 있다. 벡터 중 에센스가 모멘텀이다. 크기와 방향이 있다. 따로 계산해야 한다. 파인만다이아그램은 모멘텀이 꺽여졌다. 모멘텀 방향이 바뀌었다. 방향이 바뀌는 포인트가 vortex이다.
모멘텀을 바꾸지 않고 하는 이동이 평행이동이다. 평면에서 평행이동하여 제자리로 돌아오면 방향이 안 바뀐다. 축구공 껍질에서 평행이동 시키면? 이것 하나로 일반상대성 이론이 시작한다. 축구공 껍질에 남극점에서 시작해서 다시 남극점으로 오면 90도 바뀐다. 내가 돌은 평면이 얼마나 울퉁불퉁한가를 폐곡선을 따라 돌면 각도가 나오는데 그것이 곡률이다. 곡률보다 더 우선하는 것은 벡터를 평행이동 시킨 것이다. 곡면에서 벡터를 이동시켜 원점으로 돌아오면 기울어진 각도로 곡면의 요동 정도를 알아낼 수 있다. 북극성을 보면서 고래등을 타고 슬라이딩 하는데, 내 시선의 방향이 바뀐 것을 측정하면 고래등이 얼마나 휘었는가를 알 수 있다. 벡터가 물리학에서 모멘텀이다. 물리학은 90%가 모멘텀에 관한 것이다. 일반상대성 이론은 90%가 모멘텀에 관한 것이다. 입자물리학도 90%가 모멘텀에 관한 것이다. 모멘텀의 시간 성분이 에너지이다.
#1
오늘부터는 일반상대성 이론으로 가는데 주변까지 해서 물리학 전반을 훑어보려고 한다. 오늘 푸는 요 방정식은 가장 물리학답고 가성비가 높아 먹을 것이 많다. 지금부터 1시간 유도하는 방정식을 따라오면 이 속에 물리학 방정식 10개가 들어있다. 이 방정식의 최대장점은 어렵지 않다. 이 방정식은 10개가 어떻게 들어갔는지 파악할 수 있고, 그것이 안되도 최종결과식만 암기해도 그 공덕이 어마어마하다. 빅뱅을 알게 된다. 좋아하지 않을 수 없는 방정식이다.
멀뚱멀뚱하지 마라. 알고 모르고가 아니고 느낌이 오면 정확하게 표현을 해 주어야 한다. 표현밖에 없다. 브레인이나 물리학을 공부해 보면 표현밖에 없다는 것을 알게 된다. 내용이 있다고 생각하는 사람은 하수이다. 내용은 유인책이다. 궁극적으로는 아무 내용이 없다. 유일하게 있는 것은 껍질이다. 표현밖에 없다. 에델만의 <세컨드 네이쳐> 다시 보라. 쇼킹했다. 세계적 대가도 “궁극적으로 있는 것은 표현밖에 없으니 제발 내용이 있다는 사람은 꿈 깨라”고 한다. 전부 다 표현이다. 파깨비가 “동어반복 밖에 없다”고 하였다. 아무 것도 없다. 제발 내용 묻지마라. 내용을 묻기에 이해를 묻는다. 표현밖에 없다면 이해하고 말고 할 것이 없다.
그런 관점에서 이 방정식을 이전에 두 번 했다. 이 방정식을 풀고나면 보너스가 뭔지부터 알려준다. 이 이야기를 맨 처음 해서 세계적 스타가 된 사람이 있다. 스티븐 호킹이 <시간의 역사>로 인기를 끌었는데, 후기에 이 분야의 세계적 명저는 와인버그의 <태초의 3분간>이라고 하였다. <태초의 3분간> 전체 내용의 에센스가 빅뱅 후 알파입자 만들기까지의 과정을 풀어서 쓴 것이다. 대학교 때 읽고 쇼킹했다. “아 이렇게 하면 빅뱅을 숫자적으로 해결이 되는구나?” 물리학과 학생이 아닌 유학생이 이 책을 서점에서 사서 너무 놀라서 집까지 걸어가면서 다 봤다고 하였다.
이 세계적인 저술이 직선 방정식만 알면 끝난다. 시간에 대한 온도 직선식이다. 이 방정식만 알면 우주에서 가장 중요한 7가지 사건을 다 설명할 수 있다는 것이다. 이 방정식은 천체물리학과 교과서에 나온다. 이 방정식만 암기하면 스탠퍼드 책을 통째로 암기하는 것 이상이다. 이 방정식이 우주초기를 설명할 수 있는 이유가 방정식 속에 10개 정도의 방정식이 들어가 있다. 지난 100년 동안 핵심방정식이 다 들어있다. 그러면서도 어렵지가 않다.
열역학 제1법칙으로부터 시작한다.
U=Q-W
U는 내부에너지, Q는 열, W는 일이다. 내연기관에서 시작하였다. 폭발하면 실린더의 피스톤이 움직이면 압력이 바뀐다. 휘발유가 에너지는 퍽 하면서 열이 나오고 열이 팽창하면서 식는다. 팽창할 때 압력이 생긴다. 압력으로 팽창하면 열이 떨어진다. 피스톤이 하는 것이 일이다. 일을 하면 열이 식는 경험법칙이다.
미분형태로 적으면
dU=dQ-PdV+μ∆N
실린더 공간의 부피가 V이고, 피스톤이 움직이면 압력 P가 생기고 V가 바뀌는 것이 PdV이다. 그것이 일 W=PdV이다. 또한 큰 꽃밭에서 작은 꽃밭으로 에너지(∆E)도 주고, 비료(∆N)도 준다. 입자를 주는 개념이 ∆N이다. ∆N에 chemical potential μ를 곱해주면 μ∆N을 붙이면 생화학도 설명할 수 있다. 모든 열역학을 푸는 문제는 열역학 제1법칙의 방정식이다. 자연과학 5개 방정식 중에 들어간다.
초기에 빅뱅이 터졌을 때는 Radiation밖에 없었다. 그래서 RDU(Radiation dominant universe)라고 한다. 다음에는 물질이 생기는데 MDU(Matter dominant universe)라고 한다. 지금 우리가 사는 우주는 ⋀DU(Lambda dominant universe)이다. RDU는 빅뱅 후 5만 5천년까지이다. MDU와 ⋀DU 경계는 빅뱅 후 98억년으로, 지금으로부터 40억년 전이다. 와인버그의 <태초의 3분간>은 RDU를 푸는 것이다. 복사밖에 없었다. 이 방정식이 파워풀한 것은 우리는 지구 속은 몰라도 태양 속은 알기 때문이다. 정확히 태양 속 같다. 전부 다 복사이기 때문이다. 그래서 모두 열역학으로 다루어야 한다. 압력이 중요하다. 빅뱅 후 5만 5천년 까지는 MDU와 ⋀DU는 없다. 그래서 RDU만 다루면 되고, 뜨거운 태양일 뿐이다. 계산이 명료해진다. 첫 번째, 우주의 끝이기에 dQ=0이다. 바깥에 우주가 없으니 열교환이 안되기 때문이다. 이것을 ‘단열팽창’이라고 한다. 두 번째는 입자교환도 없다. 그래서 ∆N=0이다. 내부에너지(U) 전체는 E=mC2과 등가이다. 또한 팽창하고 있으니 압력이 있다. 그래서 에너지와 압력으로 풀어내는 것이다. 조건이 선명하다.
단열팽창 조건에서 dQ=0, 입자교환이 없으니 dN=0이다. 따라서 dU=-PdV가 된다.
dU+PdV=0를 풀면 초기우주는 맞을 수밖에 없다.
‘밀도(ρ)=질량(m)/부피(V)’이다. 그래서 m=ρV이다. 초기우주는 구이므로 부피(V)=(4/3)πR3이다. 하나도 어렵지 않다. U와 V만 알면 다 풀 수 있다.
따라서 U=mC2=(4π/3)R3ρC2 이고, V=(4/3)πR3이다.
지금부터는 미분을 한다. 미분해서 0되는 것 빼면 된다. 변수는 R과 ρ밖에 없다. 초기우주가 팽창하니 반지름이 바뀌고 밀도가 바뀐다.
dU=(4π/3)3R2R’ρC2+(4π/3)R3ρ’C2 이 된다. 이때 ‘은 시간에 대한 미분이다.
dU+PdV=(4π/3)3R2R’ρC2+(4π/3)R3ρ’C2+P(4π/3)3R2R’=0 이다. 간단하다.
계산은 공통부분 (4π/3) 제거해준다. 그리고 1/R3C2을 곱해준다.
그러면 3(R’/R)ρ+ρ’+3(R’/R)(P/C2)=0에서 순서를 정리하면
ρ’+3(R’/R)ρ+3(R’/R)(P/C2)=0 이 된다.
R은 반지름이고 R’은 반지름 증가율이다. 그래서 허블법칙이 필요하다. 빅뱅에서부터 RDU 우주이다. 이 시스템의 총에너지(E)를 본다. 로케트를 쏜다면 RDU 덩어리의 중력이 위치에너지, 로케트 올라가는 것이 운동에너지이다. 올라갔다가 당기는 힘과 동일할 때 떨어진다. 만유인력은 당기는 힘이라 –를 붙인다. 따라서 E=(1/2)mv2-(GMm)/r 이 된다. 만유인력의 M은 큰쪽의 질량, m은 test mass이다. 따라서 M은 RDU전체이다. 초기우주에서 방정식을 풀기 위해 (R’/R)값을 알아야 한다.
E=T+V=(1/2)mv2-(GMm)/r 이다. 임계치에서는 ‘운동에너지=중력’이므로 총에너지 E=0이다.
허블법칙은 v=Hr이다. H는 허블상수이고, 멀어지는 속도(v)와 거리(r)의 비이다. M=ρV이다.
집어넣으면, E=(1/2)mH2r2-(Gm/r)(4/3)πr3ρ=0가 된다.
정리하면, H2=(8πG/3)ρ로 주어진다. 우주론은 이 공식에서 나온다.
#2
다음에 필요한 공식은 photon에 의한 복사공식 P=wρC2 이 있다.
w값은 RDU에서는 1/3, MDU에서는 0, ⋀DU 에서는 –1이다. P는 빛 압력이다. 태양이 지구질량의 30만배이다. 태양중심은 2천만도 이상이다. 그러면 핵융합은 태양 중심에서 일어나므로 태양 한가운데에서 γ선이 나가는 압력을 계산하면 어마어마하다. 지구표면에서 태양빛을 미는 것은 있을 수 없는 일이다. 그런데 태양 속에 가면 달라진다. 빛의 압력이 100만기압 오더이다. 그 안에 있으면 짜부라든다. 태양질량의 100배 이상 되는 천체가 만들어지기 어려운 이유가 빛이 나오는 압력이 파괴해 버리기 때문이다. 별을 만드는 질량한계가 복사압 때문이다. 그래서 우주론에서는 빛의 복사압이 어마어마하게 중요하다. 그것을 공식으로 만든 것이다.
앞에 공식 ρ’+3(R’/R)ρ+3(R’/R)(P/C2)=0 을 정리하면,
ρ’+3(R’/R)(ρ+P/C2)=0 이고, P=wρC2 을 집어넣는다.
ρ’+3(R’/R)ρ(1+w)=0 아름다운 공식이 나온다.
방정식 푸는 것 어렵다고 하지 마라. 찾아내고 집어넣으면 된다. 찾아내는 것은 우리가 만든 것이 아니니 암기하면 된다. 공부할 것은 없고 암기할 것만 있다. 진정한 우주를 가슴에 품으려면 누가 떠밀어도 기억할 정도로 암기해야 한다. 그냥 집어넣고 파깨비의 동어반복하면 된다, 나중에 이해는 오지마라고 해도 온다. 중력장방정식 풀 때는 δg=-ggμνδgμν는 “δg gg δg”만 암기하면 된다. 중명은 하지 마라. 할 수는 있으나 매끌매끌하다.
v=Hr 에서, v는 팽창속도이므로 dr/dt이고 이것은 r’으로 적을 수 있다.
따라서 H=v/r =(dr/dt)/r =r’/r 이 된다. 이것이 허블상수(H)이다.
ρ’+3(R’/R)ρ(1+w)=0는 ρ’+3Hρ(1+w)=0이 되고, RDU에서 w=1/3이므로,
ρ’+4Hρ=0가 된다. H2=(8πG/3)ρ 이므로 집어 넣으면,
ρ’+4(8πG/3)1/2ρ1/2ρ=0
이제 밀도ρ 밖에 없다. 반지름이 사라졌다. 그래서 밀도의 변화만 알면 된다.
정리하면, ρ’=-(128πG/3)1/2ρ3/2 이 되고, 이 미분방정식을 푼다.
ρ-3/2(dρ/dt)=-(128πG/3)1/2 이 되고,
ρ-3/2dρ=-(128πG/3)1/2dt 로 밀도함수 dρ와 시간함수 dt로 나누어 주고, 적분을 하면, 밀도와 시간이 나온다.
∫ρ-3/2dρ=-(128πG/3)1/2∫dt가 되어 적분하면 붕어빵 나온다. 적분공식 ∫xn=(1/(n+1))x(n+1)이다.
따라서 (1/(-3/2)+1)ρ(-3/2)+1)=-(128πG/3)1/2t 이다. 정리하면,
ρ-1/2=(32πG/3)1/2t 가 된다.
드디어 밀도와 시간관계를 알았다. 우리가 알려는 직선식은 시간에 대한 온도이다. 그래서 밀도와 온도의 관계를 찾으면 된다. 여기서부터 어마어마하게 어렵다. 계산이 어려운 것이 아니고 연구하신 분들이 어마어마하게 수고하였다. 막스 플랑크부터 어마어마한 사람들이 다 들어가 있고, 그것을 우리가 가져다 쓰면 된다. 제발 우리가 뭘 만들겠다고 설치지 마라. 그것을 조장하는 것이 교육풍토이다. 학생이나 연구자는 그렇게 해도 일반인들은 그렇게 하면 안된다. 그래서 일반인들은 공부해도 모르는 것이다. 우리는 가져다 쓰는 것이다.
#3
1890년대에 밀도와 온도는 어떤 관계인가? 해결 못했다. 그때 막스플랑크가 문을 열기 시작했다. 천체물리학의 복사압력에 관한 일반공식이 있다. 어떤 입자가 속도 v를 갖고 움직일 때 가로막는 면이 있다면 면이 받는 압력 P는 다음과 같다. p는 모멘텀, n(p)는 입자 각각의 모멘텀 분포이다.
P=1/3∫vpn(p)dp
다음 공식은 U(ν)=(8πν2/3)(hν/(e(hν/kt)-1)으로, 플랑크 흑체복사 공식이다.
n(p)대신 U(ν)를 집어넣어 적분을 풀면,
P=(1/3)aT4이 나온다. P는 복사압력 a는 복사상수, T는 온도이다.
같은 복사압력 P=wρC2 도 알고 있으므로, w는 RDU에서 1/3이므로, 밀도 ρ와 온도 T와의 관계가 나온다.
따라서 (1/3)aT4=(1/3)ρC2 이므로,
ρ=aT4/C2 이 되어, 드디어 밀도와 온도의 관계를 찾아냈다.
이것을 ρ-1/2=(32πG/3)1/2t 에 집어 넣으면 된다.
ρ1/2을 양변에 곱해서 정리하면,
ρ1/2ρ-1/2=(32πG/3)1/2ρ1/2t
1=(32πG/3)1/2ρ1/2t 가 되고, 여기에 ρ=aT4/C2 을 넣으면,
1=(32πG/3)1/2(aT4/C2)1/2t 가 되고,
시간(t)애 대한 온도(T)를 알고자 하므로, T를 좌변으로 넘기면
T2=(3C2/32πGa)1/2(1/t) 이 된다.
오늘도 오면서 (3C2/32πGa)을 암기하면서 왔다. 중간다리 끊어져도 끝에 도달한 지점을 알면 안전이 확보된다. 이 공식을 암기하고 나면 단위를 따지고 싶어진다. a를 상수로 빼면 그때 도약한다. 이것이 어마어마한 의미가 있었구나! 모든 공식을 이렇게 암기하라는 것이 아니다. 이 공식은 워낙 응용이 중요해서이다. 이 공식 하나만 알면 우주론이 50% 끝난다.
정리하면, T=(3C2/32πGa)1/4(1/√t) 이 된다. C, π, G, a 해당 숫자 모두 집어넣으면,
T=1.5×1010(1/√t) 이 된다.
옥동자를 낳을 수 있다. t가 100만분의 1초이면 어떤 사건이 벌어지는가?
t=10-6초를 넣으면 우주온도는 T=1.5×1010(1/√10-6)=1.5×1013 K이다. K는 절대온도 단위인데, 섭씨온도로 봐도 큰 차이가 없다. 볼츠만상수 KB=8.6×10-5eV/T 이다. 이때 T는 절대온도이다. 따라서 1eV=11600도가 된다. 따라서 1.5×1013 K는 대략 1.5GeV가 나온다. 양성자 질량이 애략 1GeV이므로 100만분의 1초일 때 우주의 복사에너지가 1.5GeV이므로 충분히 양성자를 만들어낼 수 있다는 말이다. 이것을 이해해면 <태초의 3분간> 다 이해한 것이다. 어마어마한 이야기이다. 전자는 0.51MeV이므로, 60억도쯤 된다. 공식에 집어 넣으면 언제쯤 만들어지는지 시간이 나온다. 질량만 집어넣으면 에너지 eV로 바꾸면 그 입자가 우주에서 언제 출현했는지 알 수 있다.
#4
덤으로 알야야 하는 공식이 구의 체적이다. 미분 안 해도 알 수 있는 방법이 많다. 원기둥(cylinder)을 그리고 원기둥에 가득 차는 구(Sphere)를 넣는다. 구의 반지름은 r이다. 다음으로 원뿔(Corn)을 집어 넣는다.
“Corn : Sphere : Cylinder 의 체적비는
(1/3)(πr2)(2r) : (4/3)(πr3) : (πr2)(2r) = 2/3 : 4/3 : 2 = 1 : 2 : 3 이 된다.
Sphere : Cylinder 의 체적비만 알면 구의 체적 공식을 유도할 수 있다.
2 : 3 = (πr2)(2r) : Sphere
Sphere = (4/3)(πr3) 이 된다.
원의 면적 구하는 공식도 유도할 수 있다. 원을 중심에서 피자로 나누고 위와 아래로 분리해서 붙이면 부채꼴모양이 된다. π는 원주율로 지름(2r)에 대한 둘레(l)의 비로 정의한 것이다. π=l/2r이 되고 l=2πr이다. 그래서 반쪽은 πr이고 높이는 r이 된다. 따라서 면적은 πr2이 된다. 이 공식은 미적분하지 않고 π에 대한 정의에서 나왔다.
지금까지 나온 공식 카운트 해 보자.
1) dU=dQ-PdV+μ∆N 열역학 제1법칙 공식이다.
2) (GMm)/r 뉴턴의 만유인력법칙이다.
3) (1/2)mv2은 뉴턴의 역학공식에서 나온 운동에너지이다.
F=ma=m(dv/dt)=d(mv)/dt=dp/dt이다.
E=∫Fdx=∫(dp/dt)dx=∫(dx/dt)dp=∫vd(mv)=m∫vdv=(1/2)mv2이 된다.
4) v=Hr 허블법칙이다.
5) P=wρC2 우주론 복사공식이다.
6) P=1/3∫vpn(p)dp 복사압력 일반공식이다.
7) U(ν)=(8πν2/3)(hν/(e(hν/kt)-1) 은 플랑크 흑체복사 공식으로 어마어마한 방정식이다.
8) KB=8.6×10-5eV/T 볼츠만 상수공식이다.
9) (4/3)(πr3) 은 덤으로 구의 체적공식이다.
#5
물리학에서 필요한 방정식이 첫 번째 ”뉴턴방정식“, 두 번째 ”슈뢰딩거방정식“, 세 번째 ”디랙방정식“, 네 번째 ”중력장방정식“, 다섯 번째 ”측지선방정식“, 끝이다. 이것밖에 없다. 또 하나가 있다면 ”막스 플랑크 복사공식“이다.
뉴턴방정식은 F=dp/dt 한 줄로 했다. 끝이다. 만유인력방정식도 같이 끝이다. 슈뢰딩거방정식은 손으로 푸는 사람은 드물다. 코어인 주기율표 l값이 나오는 것은 앞서 했다. 실용편에 가장 중요한 것이 l값이 나오는 것이다. 모르더라도 아는 척하면 된다. 파깨비 방식이다. 알면 안다고 쌍수를 들어 자랑하고 몰라도 답이 있다. 아는 척하면 된다. 책은 안 읽어도 사두면 된다. 이 방식이다. 이해해야 한다느니 어렵다고 하면 너무 화가 난다. 그렇게 생각하면 공부가 아니다. 잘못 알고 있다. 하나하나 끝내고 없애버려야 한다.
슈뢰딩거방정식은 70%는 풀었다. 결과만 알면 된다. 끝에 의미만 캐치하면 된다. 알아야 할 것은 HΨ=EΨ 밖에 없다. H 오퍼레이터가 상태함수 Ψ에 작동하여 Ψ가 안 바뀌고 그대로 나왔다. 이렇게 나온 E를 eigenvalue(고유치)라고 한다. 고유치는 바꾸지 않는 상수라는 말이다. 그래서 E는 에너지 상수이다. H=iħ(∂/∂t)인 것만 알면 된다. Ψ=RΘΦ 함수인데, ΘΦ를 하나로 묶어서 풀어나온 답을 Ylm이라고 한다. 여기까지는 어느 정도 푸는데, R을 푸는 방정식은 복잡하다. 그래서 결과만 알면 되는데, 수소원자 En=-13.6(1/n2) eV 이다. Ψn,l,ml,ms가 있는데, 가장 응용이 많은 것은 l값이다. 그것이 주기율표이다. ms는 +1/2ħ, -1/2ħ 딱 2가지 값만 갖는데, 우주가 생길 때부터 고유하게 갖는 값이고 왜 그렇게 되는지는 모른다. ”ms=묻지마“이다. ml은 안다. l값을 투영한 것이라 l값만 알면 자동으로 안다. l값 알면 슈뢰딩거방정식은 끝난다. ”l값=주기율표“이다.
디랙방정식은 지난 15년 동안에 3년간 풀어주었다. (γμPμ-mc)Ψ=0이다. 디락방정식은 γμ가 중요하다. 4×4 매트릭스만 읽을 수 있으면 된다. 열로 읽어서 1열은 전자의 스핀업, 2열은 전자의 스핀다운, 3열은 양전자의 스핀업, 4열은 양전자의 스핀다운이다. 디랙방정식 끝이다.
지금부터 중력장방정식 들어간다. 2008년부터 시작하여 올해 15년째 강의로 1단계 마무리한다. 더 이상 할 필요가 없다. 물리학은 다 끝낼 수가 있다. 더 이상 할 필요 없을 정도로 명확하다. 중력장방정식도 10분이면 다 푼다. 엄청나게 집어넣고 고민하고 겪어봤더니 10분만에 하는 방법론이 있다. 자연과학 공부는 끝이 있다. 5개로 끝이다. 태권도 1단과 9단의 차이는 무엇인가? 품새는 다르지 않다. 9단도 다른 자세가 없는데 실력차이가 어마어마하게 난다. 기본은 검은띠 하나로 끝난다. 더 이상 없다. 그런데 9단과의 차이는 얼마나 심었는가에서 온다. 그 사람 모든 것이 그것으로 바뀌어져야 한다. 신통묘연이 나온다. 전체 우주를 그걸로 보기 시작한다. 그 단계가 온다. 여러분은 빨리 검은띠부터 따야 한다. 그때까지는 묻지말고 그냥 품새만 익혀라. 옆차기와 찌르기만 반복하라. 그것을 반복할 시간에 자꾸 엉뚱한 것 하니 화가난다. 그것이 다 끝나면 더 이상 배울 게 없다는 것을 알게 된다. 그 다음부터는 각자 수련이다. 죽을 때까지 각자 수련해야 한다.
중력장방정식과 측지선방정식은 ‘로미오와 쥴리엣’으로 하나이다. 그래서 막스 플랑크 복사공식까지 해서 5개면 물리학 끝이다. 그것밖에 없다. 나머지는 계산과정으로 컴퓨터 돌리는 것이다. 물리학은 1년이면 끝난다. 브레인은 10년 걸린다. 그러나 물리학은 기본품새이다. 기본품새를 안 익히고 자꾸 엉뚱한 것 하려고 한다.
지금도 강의에 대해서 회원에게 물어보면 모르겠다고 한다. 내가 이 우주에서 가장 궁금한 것은 ”당신이 모르는 것이 뭔가?“이다. 모른다고 하는 사람은 뭔가 알아야 하는 것이 있다는 착각에 빠진 것이다. 그걸 깨 부서야 한다. 따로 알아야 할 것이 있는 것이 아니고 집어넣을 것만 있다. 벽돌을 쌓으라고 하는데, 안 쌓고 자꾸 엉뚱한 장난만 하고 있으니 화가 난다. 벽돌은 있으니 쌓아서 집만 지으면 된다. ”느낌이 오냐?“고 물으면 표정이 묘하다. ”알았다, 몰랐다“도 표현을 못한다. 표현이 전부 다이다. 내용은 없다. 학문은 하면 할수록 내용은 없고 드러난 것 ”표현“밖에 없다. 표현을 못하면 없는 것이다. 알고 있으면 뭐든지, 욕을 하더라도 표현을 할 수 있다. 다른 게 없다. 여기에 하나라도 신비가 있다고 생각하는 사람은 공부 잘못하고 있는 것이다. 이해할 것이 있다고 생각하는 사람은 공부 잘못하고 있는 것이다. 파깨비 유튜브를 다시 보라. 모든 수학은 ‘동어반복’밖에 없다.
”너무 쉽다. 공부할 것 없다“ 하고 들어가야 한다. 싸우는 상대에게 주눅이 든다. 아인슈타인에 대해 많이 듣다보니 주눅이 들었다. 아인슈타인은 결혼 3번 하고 50대 이후로 물리학에 기여한 것 없이 놀았다. 1915년까지 어마어마한 연구를 하고 아인슈타인의 연구인생은 끝났다. 그 이후로 헛발질 많이 했다. 너무 신비화시켜서 그렇다. 마지막에는 그냥 동네 늙은이였다. 하나도 신비한 것 아니다. 공부하는 입장에서는 성철스님도 그냥 먼저 간 선배로 생각해야 한다. 어느 측면에서는 괴팍한 노인, 이렇게 생각하면 된다. 폄하하는 것이 아니다. 우리가 자꾸 이상하게 얘기하니 실체를 못 보기 때문이다. 그 사람도 배고프고 그냥 그런 거다. 아인슈타인 아들도 정신병으로 비참하게 되고, 첫 아내는 이혼하고 노벨상 받은 상금을 주고, 두 번째 아내는 연구에 기여했다고 하는데 그것도 잘 모르고 하는 이야기이다. 아인슈타인은 너무 괴팍했다. 세 번째 결혼하고 섬씽이 무지 많다. 그러함에도 불구하고 인류역사상 위대한 인물이다. 이러한 사생활이 없이 위대하면 인간도 아니게 된다. 그런 점이 있어 오히려 인간적으로 보인다.
아인슈타인이 중력장방정식 유도하는 과정은 그가 결코 뛰어난 수학자가 아니었음을 보여준다. 10년 동안 했다. 다 증명하고 봤더니 그 전에 누군가가 다 해 놓았다. 모세(Moses, BC1527~BC1406)가 40년 동안 시나이반도 사막을 헤맨 이유는 길을 안 물어봐서이다. 아인슈타인도 물어보지 않아서이다. 비앙키항등식을 증명하는 과정이다. 옆에 안 물어보고 혼자 낑낑거려 10년 동안 엄청 고생했다. 아인슈타인 사생활은 굉장히 괴팍했으나 한가지 특징은 연구를 물고 늘어지면 10년 이상 물고 늘어졌다. 광양자가설을 가장 오랫동안 끝까지 물고 늘어졌다. 중력장방정식도 10년 물고 늘어졌다. 우리는 그렇게 안 해도 된다. 아인슈타인이 한 것을 10분 만에 할 수 있다. 결과 암기하고 헛발질 안하면 된다.
4차원 세계로 들어가야 한다. 특수상대성 초반부에 나오는데, 대충 있다고 넘어가는데 공부하면 할수록 이 간단한 4가지를 철저히 안해서 헷갈린다.
4차원 위치벡터 X-> 부터 한다. 벡터는 크기와 방향이 있다. 절대값을 취해주면 벡터의 크기를 계산하는 것이다.
lX->l=√(X->X->)로 정의한다.
X->를 표현하는 방법은 시간텀과 공간텀으로 나누어주어
X->= (ct, x)로 적는다. x는 공간, ct는 시간차원이다.
민코프스키 시공간 정의에 따라 4차원에서는 피타고라스 정리가 √x2-y2이 된다.
따라서 4원 위치벡터의 크기는
lX->l=√(ct)2-x2)이 된다.
4원 속도벡터(U)는 고유시간(τ)이 들어간다. dX->= (cdt, dx)이다.
따라서 U=(dX->/dτ)=(d/dτ)(ct, x)=(c(dt/dτ), dx/dτ) 가 된다.
특수상대성에서 t=τ/√1-(v/c)2 이다. τ는 고유시간(proper time)이다. v->C로 가면 v->무한대로 간다. v->0로 가면 t=τ 이다. 따라서 고유시간은 속도가 0인 상태에서 잰 시간이다. 속도가 0인 상태의 시간은 여러분이 여러분의 손목시계를 본 것이다. 손목시계는 나에 대해 움직이지 않는다. 관찰자가 본 시간으로 관찰자와 같이 움직이므로 상대속도가 0이다. 내가 달리는 기차의 시계를 볼 때 그 시간은 t이고, 내가 내 시계를 볼 때 시간은 τ이다.
1/√1-(v/c)2을 γ라고 부른다. 따라서 t=γτ이고, 미분하면 dt=γdτ 가 된다.
따라서 dt/dτ=γ 이다.
dx/dτ=(dt/dτ)(dx/dt)가 되고, dx/dt가 통상속도 v이다.
따라서 dx/dτ=γv 이다.
따라서 U=(c(dt/dτ), dx/dτ)=(Cγ, vγ)이다.
#6
IUI=√(U->U->)=√(Cγ)2-(vγ)2 = γ√C2-v2 = γC√1-(v/c)2 이다.
√1-(v/c)2 = 1/γ 이므로,
IUI=γC(1/γ)=C가 된다.
브라이언 그린(Brian Greene, 1963~)은 <우주의 구조>에서 지금 이 IUI=C 라는 결과가 E=mC2 보다 더 중요하다고 하였다. 4차원 속도벡터의 크기가 광속이다. 4차원의 모든 존재는 광속으로 움직인다는 것이다. 이것이 무슨 말인가? 나는 정지해 있는데? 우리는 4차원 세계에 살고 있다. 4차원 세계에 있는 모든 존재가 광속도라는 것이 실감 안 된다. 시간축(ct)과 공간축(x)이 있다면 속도벡터(U)의 크기는 광속(C)이다. 빛은 광속도로 달린다. 따라서 공간축에 100% 그대로 투영된다. 만일 광속의 90%로 달린다면 공간축에 90%, 시간축에 10% 와 있게 된다. 우리는 공간축에 속도는 0에 가깝다. 만일 정지해 있다면 시간축에 100% 붙는다. 그러면 시간의 속도는 광속이다. 세월의 속도는 광속이다. 4차원 존재는 정지해 있는 존재는 없다. 속도는 딱 하나 광속밖에 없다.
지금 온갖 과학이 폭발하고 있는데, 모든 것을 합쳐도 딱 하나만 인류가 정확하게 캐치하면 죽음 이후의 문제 등 모든 것을 한꺼번에 끝낼 수 있는 후보가 있다. 우리는 4차원 시공 속에 산다. 1차원 시간과 3차원 공간 속에 사는 것이다. 우리는 4차원 공간은 모른다. 블랙홀 속은 5차원이다. 공간 4차원+시간 1차원이다. 그 세계는 블랙홀 들어가기 전에는 모른다. 그것에 대한 과학계의 힌트가 무엇인가? 2차원에 사는 개미를 공중에 띄워 옮기면, 공중에 떳다라는 개념은 개미에게 없다. 이와 똑같은 상황이다. 우리는 3차원 공간에 살고 있어 4차원 공간 냄새를 맡을 수 없다. 그런데 과학이 몸부림치다가 4차원 공간이 존재할 수 있는 간접적 추론을 할 수 있는 증거가 나왔고 그 유튜브가 있다. 양자홀효과(quantum Hall effect, QHE)이다. 마그네틱 실험조건에서 전자가 딱 한 줄만 가는데, 다른 차원의 공간이 끼어들지 않고는 과학적으로 일어날 수 없는 현상이다. 다른 예는 닐스보어 원자모델에서도 알 수 있다. 전자가 다른 궤도로 올라갈 때 시간이 얼마 걸리는지 얘기를 안 한다. 순간도약이라고만 한다. 아인슈타인이 평생 이야기한 것이 순간적 현상이 없다는 것이 현대과학의 근본이다. 이것이 무슨 말인가? 전자의 점프에 대한 어떠한 방정식도 없는데 일어나고 있다. 어떤 설명도 할 수 없는데 일어나고 있다. 개미가 가는데 누군가 집어서 옮겨 놓으면 개미 입장에서는 설명은 할 수 없는데 갑자기 저기로 갔다고 얘기할 수 있다. 정상과학 속에도 모르는 차원이 끼어든 것이 아닌가 조금 냄새를 맡아볼 수 있는 것이 1-2개 있다. 지금 과학에서 차원의 비밀이 풀리면 시간여행은 낮잠자고 일어나는 정도의 게임 밖에 안된다. 하나도 신기한 현상이 아닐 수 있다. 사후의 세계, 종교의 깨달음도 차원의 놀라움에 비하면 아무것도 아니다. 차원의 문제가 풀리면 우리는 달라진다.
물리학에서 차원의 문제가 어마어마하다는 것을 나타내는 방정식이 E2=(pC)2+(m0C2)2이다. 지금 얘기한 5개 방정식이 다 여기서 나온다. 섬찟해야 한다. 어떻게 가능할까? 물어봐야 한다. 이것을 처음 낌새챈 사람이 아인슈타인이었고, 칼루자(Kaluza)와 클라인(Klein)이 아인슈타인의 논문을 5차원을 상정해서 풀면 간단히 풀린다는 것을 보여주었다. 아인슈타인은 그 논문을 2년 동안 서랍 속에 묻었다. 아인슈타인도 이것이 어마어마한 충격을 주는 논문이라는 것을 알았다. 아인슈타인이 문제를 푼 것도 4차원으로 올려서 풀린 것이다. 그런데 만일 5차원 시공이 있고 4차원 존재에게 영향을 준다면 사후의 세계나 도를 깨치는 문제가 바로 옆집에 있을 수 있다. 우리가 밥먹고 대소변 보는 일과 똑같아진다. 과학이 올인해야 할 문제는 궁극적으로 차원의 문제이다. 평행우주론 등의 문제가 다 차원의 문제에 들어가 있다. 일반상대성 이론도 인류 최초로 차원의 문제의 문을 열었던 것이다.
차원으로 들어가면 유도할 필요가 없다. 그냥 나와버린다. 앞으로 물리학이 모두 끝날 수 있다는 것이 딱 한가지 라그랑지안이다. 그 하나로 다 풀린다.
다음은 4원 모멘텀(P)으로 간다. 정지질량(m0)에 4차원 속도벡터(U)를 곱해주면 된다.
P=m0U
IPI=√P->.P->= √m0U.m0U = m0√U.U = m0C
장난같다. 차원을 올리면 미분적분도 필요없고 간단히 답이 나온다.
다시 다른 정의로 풀면
P=m0U=(m0γC, m0γv)
m=m0γ이므로
P=(mC, mv)가 되고,
IPI=√P->.P->= √(mC)2-(mv)2 = √(mC2/C)2-(p)2 = √(E/C)2-(p)2 이다.
따라서 두가지 P 풀이를 비교하면,
m0C = √(E/C)2-(p)2 , 제곱하면, (m0C)2 = (E/C)2-(p)2
정리하면 E2=(pC)2+(m0C2)2이다.
슈뢰딩거방정식, 디랙방정식, 맥스웰방정식 등 대부분 방정식이 이 방정식에서 유도된다. 4차원에서 나왔기 때문이다.
#7
중력장방정식은 잘 따라오면 5줄만에 끝난다. 10분만에 할 수 있다. 물리학은 끝이 있다. 내년부터는 플랫폼이 다 되었으므로 물리학방정식 5개를 몸으로 숙달하는 훈련과정을 하고 싶다. 이 방법으로 하면 물리학 석사수준을 1년 만에 끝낸다. 그렇게 하려면 한달 동안은 묻지말고 내가 하는 ‘델지지지델지’ 방식으로 암기해야 한다. 암기하는 대못을 뽑고 나면 10분만에 끝난다.
gμν는 매트릭텐서이다. IgμνI 행렬값(determinant)은 4×4 계산은 복잡하다. 행렬값(determinant)은 행렬이 하나의 숫자로는 어떤 값인가를 구하는 것이다. gμν 행렬값이 g이다. δg는 그 변분이다. 그래서 매트릭텐서의 행렬값을 구히고 그 값의 변분을 구하는 것이 중력장방정식의 90%이다. 그래서 ‘델지지지델지’만 기억하면 90% 풀린다. 이것만 따로 계산하는 과정이 30-40분 걸린다.. 2019년 강의노트 참조(제11회 137억년 우주의 진화 3강 노트)하면 된다.
모든 것은 라그랑지안에 들어있다. 라그랑지안을 공간에 대해 적분하면 작용이 된다. 우주의 구조는 작용이 결정해준다. 작용의 parameter가 플랑크상수이다. 최소작용의 법칙 δS=0을 쓰면 중력장방정식이 나온다. 힐버트방식이다. 작용은 두 가지이다. 우주는 물질이고 진공이 있다. 진공(Vacuum)의 작용을 Sv, 물질(matter)의 작용을 Sm이라 하면, S=Sv+Sm 이 되고, S에 대해 변분 δS를 취해주고, δS=0가 되는 조건을 찾아내면 되는데, 그 조건이 중력장방정식이다.
δS를 계산하는 과정에서 가장 계산이 많은 것이 δ√-g이다. 일반상대성에서 가장 어려운 부분이다. Sv=(1/2k)∫R√-g dV 가 되는데, √-g가 뭔지가 헷갈린다. g는 매트릭텐서의 행렬값이다. 그런데 왜 –를 붙이고 √에 들어가는가? 4차원 피타고라스 정리에 –가 들어가는 것과 동일하다. V는 시간까지 들어가는 4차원 부피인데, dV는 불변량이 아니다. 호킨스의 <천개의 뇌>에서 얘기하듯이, 인간이 우주를 알게 된 것은 우주에 수천 개의 고유좌표를 부여해 주었기 때문이다. 책상에 1m 자를 붙여주면 달나라 가면 책장이 부풀어 오르는데, 자도 부풀어 오른다. 태양에 가면 책상이 쭈그러들면 자도 쭈구러들어 1m 그대로이다. 지구에서도 1m, 달에서도 1m, 태양에서도 1m, 어디를 가도 바뀌지 않는다. 이것을 불변량이라고 한다. 우주에서 부피의 불변량을 만들어주기 위해서는 √-g를 곱해주어야 한다는 것이다. dV는 불변량이 아니고, √-g dV는 불변량이 된다. √-g dV는 라그랑지안 속에 있으므로 스칼라가 된다. 스칼라가 불변량이고 대칭이고 상수이다. 인간이 바뀌지 않는 불변량을 찾는 것이 자연과학이다. 바뀌는 것(dV)은 안 바뀌게(√-g dV) 해 주면 된다. 스칼라밀도가 된다. 스칼라밀도로 4차원 시공에 라그랑지안을 계산해서 나온 작용(S)에 variation(δ)을 주어 δS=0가 되는 포인트를 찾으니 중력장방정식으로 드러난다. V의 상수를 찾는 것이다. 부피와 질량으로 밀도가 나오므로 스칼라밀도라고 한다.
힐버트-아인슈타인 작용(S)이라고 한다. 작용은 진공의 작용 Sv과 물질의 작용 Sm의 합이다.
따라서 S=Sv+Sm 이다.
진공의 작용을 설정하면, 비례상수 (1/2k)을 넣고, 라그랑지안을 적분해야 하는데, 라그랑지안으로 설정한 것이 시공의 스칼라곡률 R이다. 여기에 스칼라밀도를 구하기 위해 √-g dV를 해 주었다.
따라서 Sv=(1/2k)∫R√-g dV 이다.
Sm은 물질에 의한 라그랑지안을 설정해준다. 모르는 라그랑지안을 Lm으로 하고 불변량으로 바꾸어주기 위해 √-g dV 를 해 준다.
따라서 Sm=∫Lm√-g dV 이다.
아이슈타인과 힐버트가 이렇게 설정했다는 것이다. 1915년에 유명한 사건이다.
여기에다 아인슈타인이 나중에 우주상수(⋀)를 중력장방정식에 집어 넣는다. R 대신에 R-2⋀를 아인슈타인이 시도한 것이다. 나중에 밝혀진 것이 지금 우주가 팽창하는 진공자체의 에너지이다.
S=∫(1/2k)〔R√-g – 2⋀√-g + 2KLm√-g〕dV 로 묶는다.
변분하여 흔들어보면
δS=∫(1/2k)〔√-gδR + Rδ√-g – 2⋀δ√-g + 2Kδ(Lm√-g)〕dV
첫 번째, δR의 계산은
R=gμνRμν 이므로, δR = δ(gμνRμν) = Rμνδgμν + gμνδRμν가 되고,
δRμν의 계산은 복잡한데, 결과는 0이다. 먼저 결과부터 알고 복잡한 것은 나중에 하면 된다.
따라서 δR = Rμνδgμν 가 된다.
두 번째, δ√-g의 계산은
δ√-g = δ(-g)1/2 = 1/2(-g)-1/2(-δg) = (-1/2√-g)δg
δg의 계산은 ‘델지지지델지’로 암기하라.
δg=-ggμνδgμν
따라서 δ√-g = (-1/2√-g)(-ggμνδgμν)
g=-√-g√-g 로 바꿀 수 있으므로,
δ√-g = (-√-g√-g / 2√-g)(gμνδgμν) = (-√-g / 2)(gμνδgμν)
그 다음에 집어 넣으면 아인슈타인이 10년 동안 했던 결과가 나온다. 동어반복이 위대하다. 10년동안 했지만 우리가 다 알고 났더니 30분이면 된다. 근본은 수학적으로 동어반복밖에 한 것이 없다.
작용의 변분을 최종 계산해 본다. 쭉쭉 집어 넣으면 된다.
δS=∫(1/2k)〔√-gRμνδgμν + R(-√-g / 2)(gμνδgμν) – 2⋀(-√-g / 2)(gμνδgμν) + 2Kδ(Lm√-g)〕dV =0 조건을 찾아내면 된다. 적분 속에 값이 0가 되면 되므로,
√-g δgμν를 약분하면,
Rμν - (1/2)gμνR + ⋀gμν + 2Kδ(Lm√-g)/(√-g δgμν) = 0
Rμν - (1/2)gμνR + ⋀gμν = K〔-2δ(Lm√-g)/(√-g δgμν)〕 가 된다.
〔-2δ(Lm√-g)/(√-g δgμν)〕 값은 모르므로, Tμν로 둔다.
그러면, 중력장방정식은,
Rμν - (1/2)gμνR + ⋀gμν = KTμν 가 된다.
K상수는 푸와송방정식과 비교해서 찾아낸다.
그러면 K=8πG/C4가 된다.
#8
측지선방정식은
dP->=0 , P->=Pμeμ 로 표시한다. 평행이동이다.
dP->=d(Pμeμ)=d(Pμ)eμ+Pμdeμ 이다.
deμ = ⌈μνρdxνeρ 를 넣으면
dP->= dPμeμ+Pμ(⌈μνρdxνeρ)
여기서는 묶기 위해서 인덱스 ‘ρ <-> μ’ 를 서로 바꾸어 준다.
dP->= dPμeμ+Pρ(⌈ρνμdxνeμ) = (dPμ + Pρ(⌈ρνμdxν)eμ
측지선 방정식은 최단거리이므로 벡터를 안 바꾸고 평행이동시킨 것이다. 그것의 수학적 조건이 dP->=0가 되는 것이다.
따라서 (dPμ + Pρ(⌈ρνμdxν)eμ = 0 이 된다.
다음은 Pρ=m(dxρ/ds)로 정의하고 집어 넣고, d/ds로 미분을 해주면,
(dPμ/ds + m(dxρ/ds)(⌈ρνμ(dxν/ds) = 0
매끌매끌해서 훈련해야 한다.
다음은 u=dx/ds, dPμ/ds=m(du/ds) 이므로,
m(du/ds) + m(⌈ρνμ(dxρ/ds)(dxν/ds) = 0
(du/ds) + ⌈ρνμ(uρuν) = 0
이것이 측지선방정식이다.
대충 이런 이야기이다. 이 방정식은 운동방정식이다. 태양 질량에 의해 시공이 휘어지는 정도를 Rμν 로 계산하는 것이 중력장방정식이고, 휘어진 시공의 곡률을 따라 지구, 화성이 도는데, 그 행성들이 가는 운동방정식이 측지선방정식이다. 어마어마한 방정식이다. 그래서 둘이 쌍으로 되어 있다. 다음 시간에 더 상세히 설명한다.
마무리하면, 어마어마한 것 했다. 중력장방정식 간단하다. 몇줄 안 된다. 해 놓고 뿌듯하다. ‘델지지지델지’ 암기 안 하면 풀 수 없다. 뉴턴방정식, 만유인력방정식, 슈뢰딩거방정식, 디랙방정식 했다. 지난 2주 동안 했던 것이 디랙방정식부터 시작한 입자물리학을 다룬 것이다. 오늘 ‘중력장방정식’과 쌍이 되는 ‘측지선방정식’ 했다. 측지선방정식 유도하는 것도 저것 말고는 1시간 해야 한다. 너무 복잡하다. 저것은 훈련하면 10분 만에 할 수 있다. 다음에 플랑크복사곡선 구하는 것도 했다. 다 했다. 내년에는 이 5개 방정식을 2시간 만에 여러분들이 다 발표하는 것을 해 보고 싶다. 입자물리학도 더 훈련해야 하고, 중력장방정식은 인덱스 바꾸는 것과 매트릭텐서 의미를 다음 시간 좀 더 하고, 그러면 15년째 이 강의, 물리학 강의는 이 이상 더 없다. 이 이상 더 있는 분야는 계산기로 해야 한다. 그래서 학문에 끝이 있다. 브레인, 세계사에 적용하고 싶으면 완전히 사무쳐야 한다. 일반상대성 공부한 것이 세계사에 투영이 된다. 브레인 공부에도 직접 연결된다. 소뇌의 이론가 중 처칠랜드(Churchland)가 있다. 소뇌에서 일어나는 일을 일반상대성 이론 공식을 써서 논문을 썼다. 소뇌에서 브레인 신경작용은 메트릭텐서와 비슷하다고 하여 주류는 아닌데 논문도 나오고 히트를 쳤다. 소뇌에서 일어나는 일을 일반상대성 로테이션을 써서 설명해야 한다는 데까지 올라와 있다. 응용이 무궁무진하다.

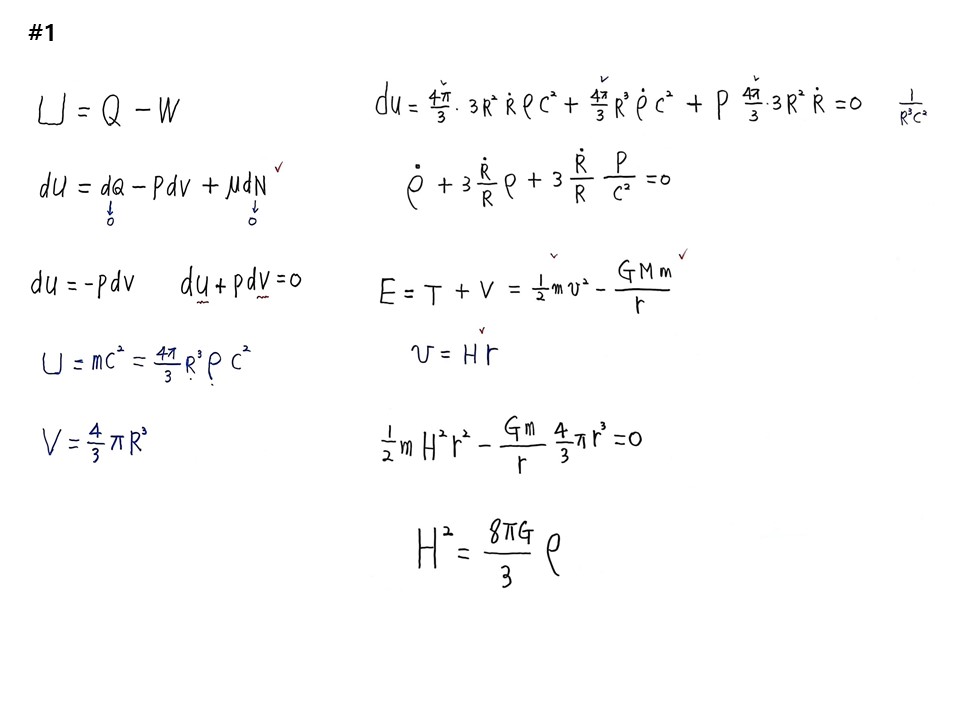
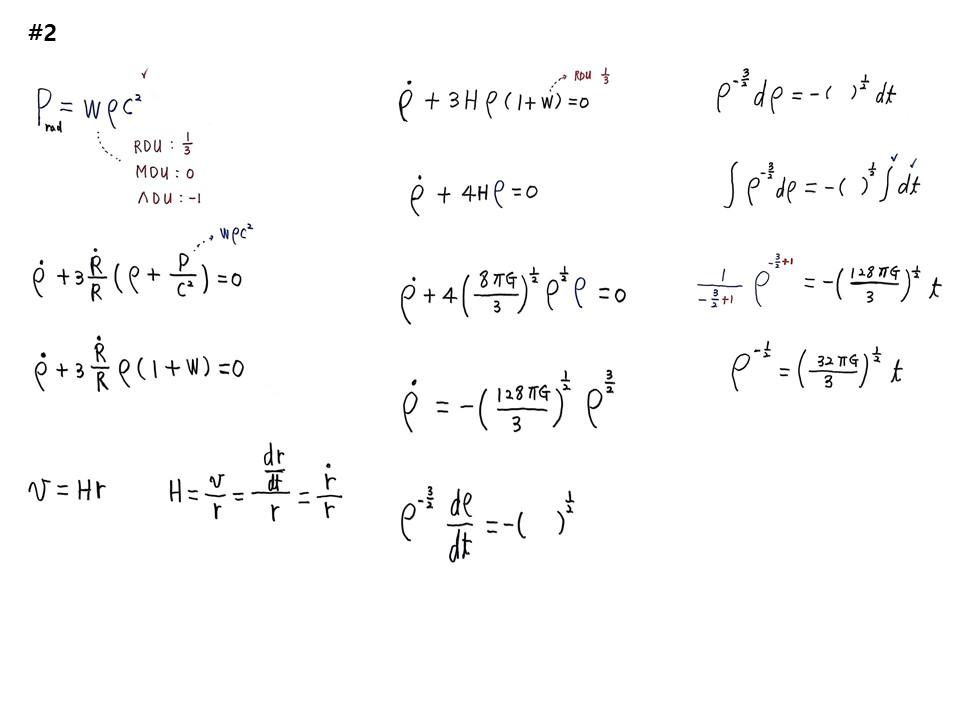
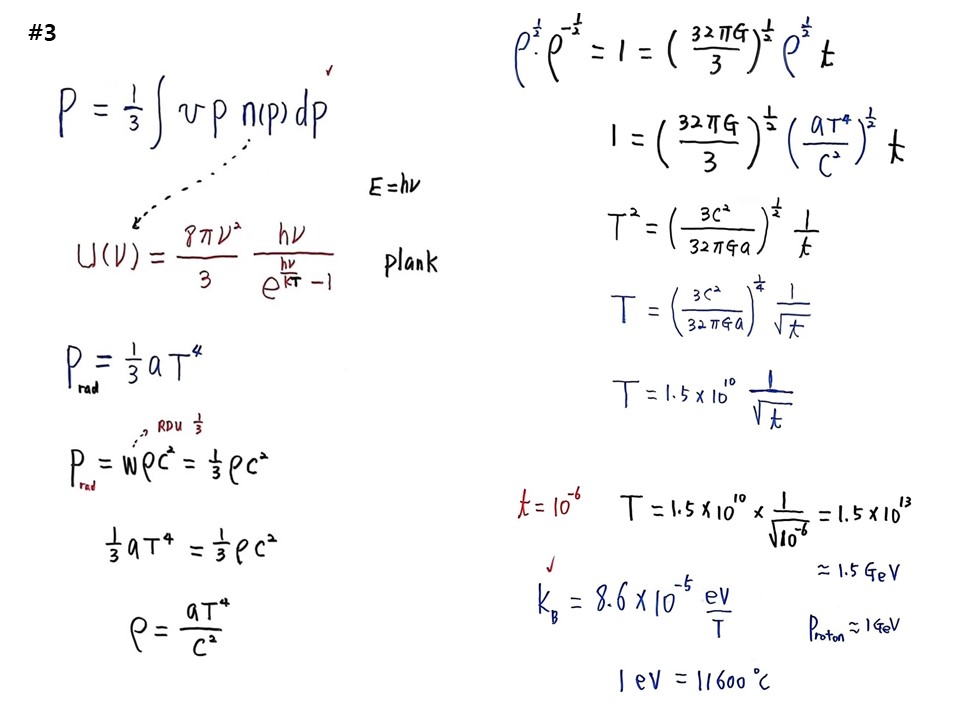

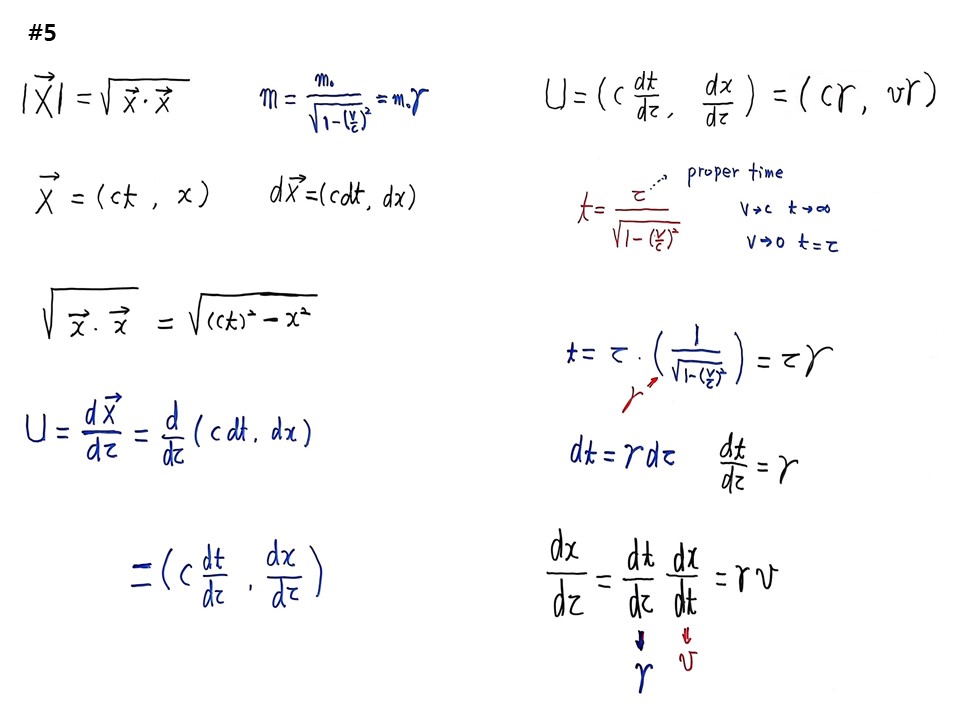

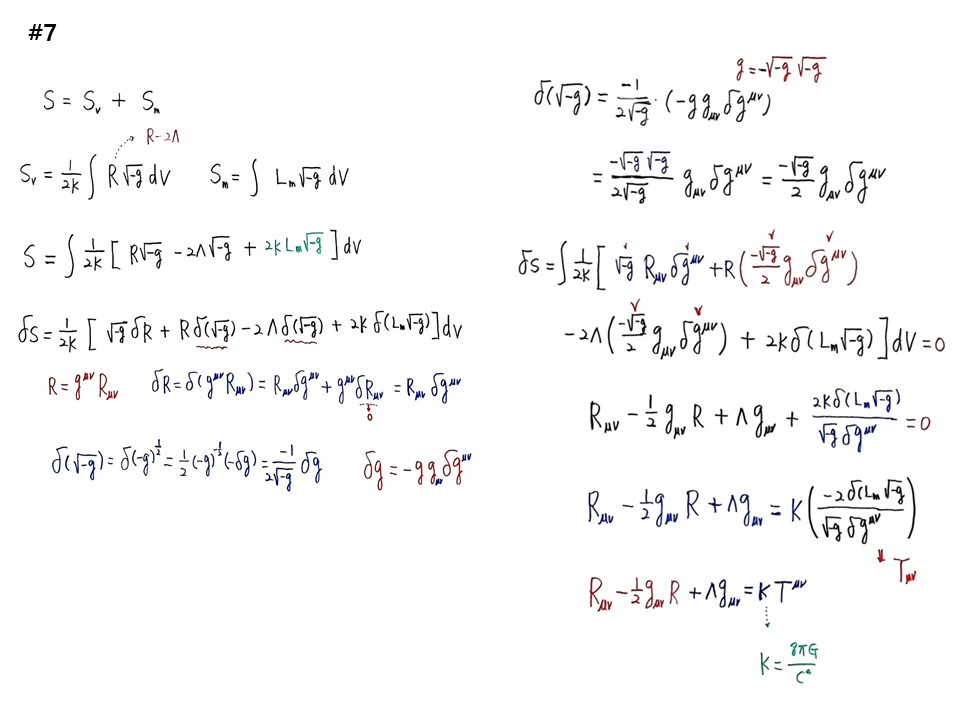
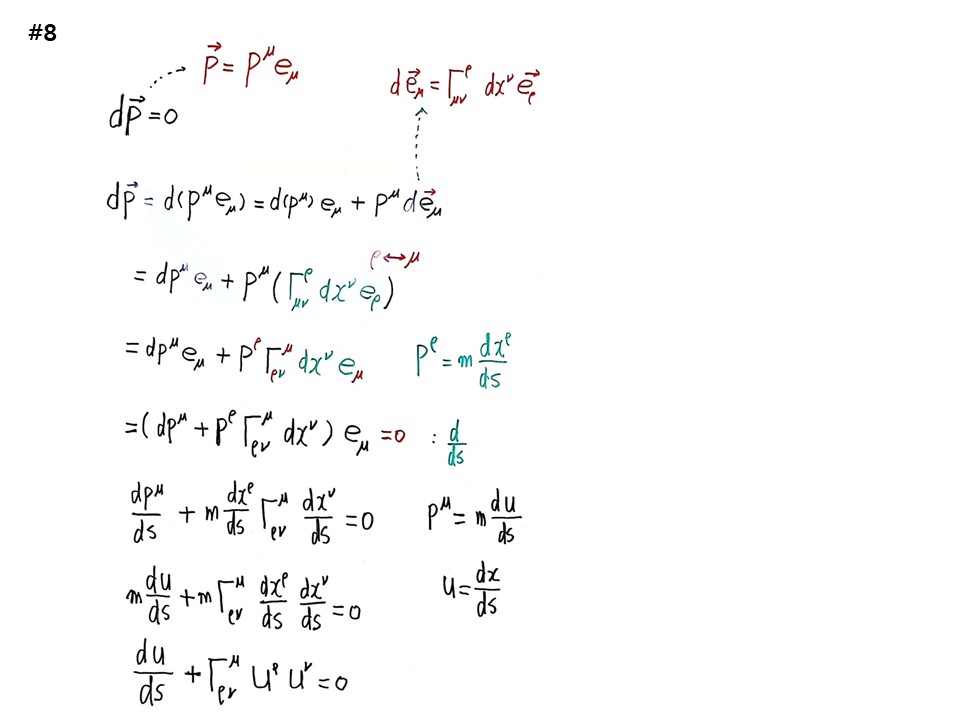
감사합니다!!