수업후기
#6
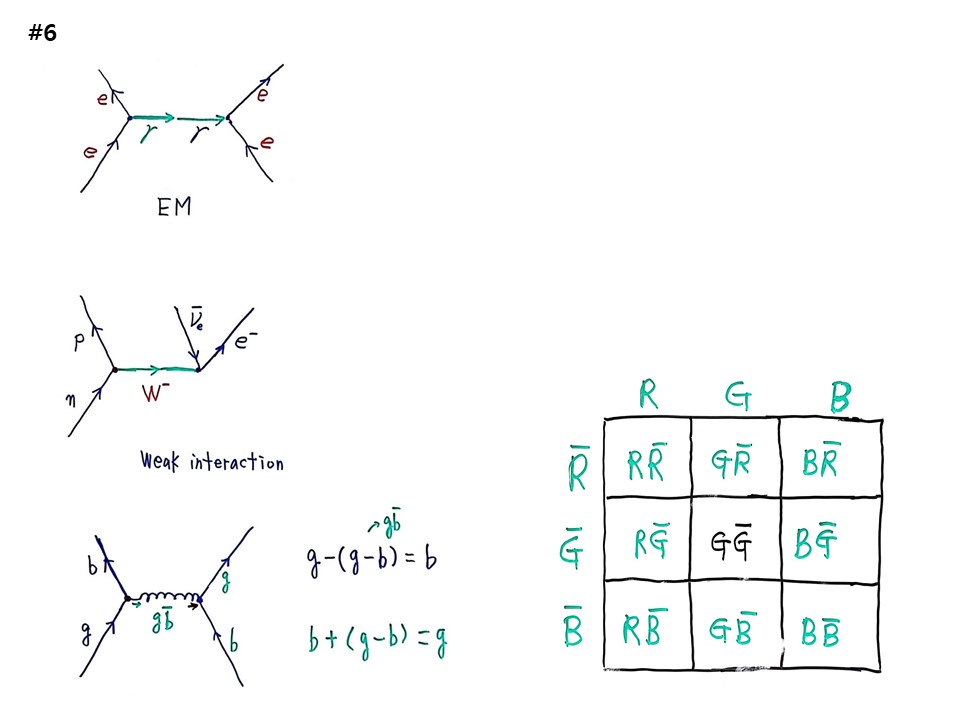
오늘이 큰 산맥이다. 자연과학에서 만나는 최고 난이도 높은 계산이다. 인간이 여기까지 왔다는 것이 대단하다. 무슨 말인가하면, 역사적으로 알야야 한다. 지금부터 그리는 다이아그램 3개 속에 다 들어있다 주기율표, 별이 불타는 것, 세포가 작동하는 것 다 들어 있다. 유명한 ‘파인먼 다이아그램’이다. 자연과학은 이 3개 밖에 없다. 너무 단순해서 중요함을 모른다. 전자는 가까와지면 서로 밀어내는데 어떻게 밀어내는가? 이것을 이해한 것이 100년도 안된다.
물리학은 2가지 이야기 밖에 없다. 에너지와 모멘텀이다. 더 확률이 높은 것은 모멘텀이다. 벡턱 나오면 모멘텀이다. 모멘텀은 집합론적 사고에서 더 위 차원에서 보면 벡터이다. 벡터는 방향이 있다. 가까이 접근하는 거나 멀어지는 것은 방향이다. 밀어낸다는 것은 멀어진다는 것이다. 가까워지기에 멀어진다. 안 밀어내면 충돌한다. 밀어냈기에 방향이 바뀐다. 벡터이다. 앞에 한 모든 방정식은 스칼라 속에 다 들어있다. 가까이 와서 붙을 수 있는데 밀어낸 것은 붙지 않았다는 말이다. 가까이 왔는데 왜 멀어졌는가? 둘 사이 무슨 일이 있었는가? 그 이야기이다.
첫 번째는 진공 속에서 전자가 서로 가까워지는 벡터에서 멀어지는 벡터로 바뀐다. 이 사이에는 뭔가 작용을 한 것이다. 전자는 광자를 방출한다. 애기 업은 엄마가 애기를 던지면 그대로 못가고 휘청거린다. 전자가 광자를 던진 것이다. 누가 애기를 던지니 지나가던 사람이 애기를 받았으니 그대로 못 가고 휘청인다. 그래서 벡터가 바뀌어 간 것이다. 이것을 계산하는 것이다. 이때 작용한 힘을 전자기력(EM force)이라고 한다.
두 번째는 중성자가 가다가 꺽여지면서 양성자로 바뀌었다. 어떤 사건인가? 전하량이 바뀌었다. 중성자에서 전하량을 뱉어 내었다. 전하량을 삼키는 애가 진공에서 나타난다. 시간을 거슬러 미래에서 현재로 다가오던 입자가 전하량을 삼켜버리고 났더니 모멘텀이 바뀌어 튕겨서 나갔다. 다가오던 애는 전자뉴트리노의 반물질이고 튕겨져 나간 것은 전자이다. 이 그림에 주기율표가 다 들어있다. 뱉어낸 전하량이 W-입자이다. 전자의 전기량 –는 W-에서 나간 것이다. 이것을 약력(Weak force)라고 한다.
지금까지 전자기력과 약력이 결합된 상태를 푼 것이다.
세 번째는 green gluon(g)이 가서 blue gluon(b)이 되었다. 모멘텀이 바뀌면서 뭔가 방출되었는데, 진공에서 b가 들어와서 g가 되어 나갔다. 이때 방출된 것은 gbbar이다. g점에서는 (g-b)가 나가서 g-(g-b)=b가 된 것이다. b점에서는 (g-b)를 받아들였다. 그래서 b+(g-b)=g가 된 것이다.
이때 글루온 8가지는 도표처럼 되어 있다. 반물질은 bar를 붙여준다. R-G-B와 Rbar-Gbar-Bbar를 가로 세로로 놓고 그려주면 9개가 나오는데, 한가운데 GGbar는 없으므로 8개가 된다. 원자핵 속에서 광속도로 움직인다. up-quark, down-quark의 칼라를 바꾸어준다.
#7
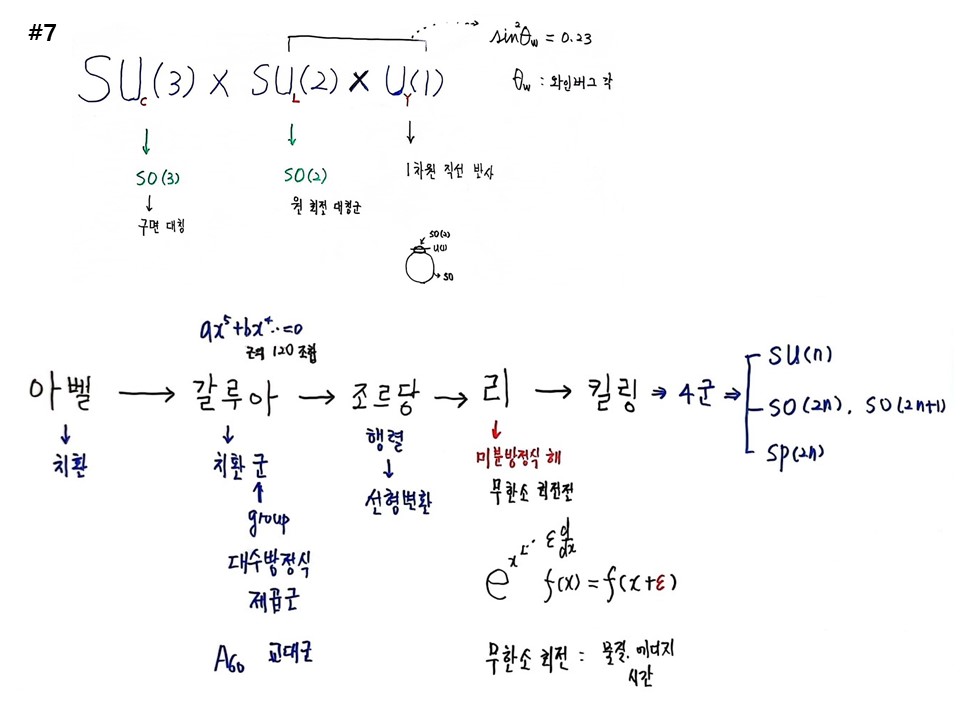
입자물리학에 인류가 얻은 최종결론은 “SUC(3)×SUL(2)×UY(1)”이다. 족보는 SU(3)는 SO(3)에서 SU(2)는 SO(2)에서 왔다.
수학사의 족보를 알아야 한다. “아벨 -> 갈루아 -> 조르당 -> 리 -> 킬링” 이다. 아벨은 치환이다. 갈루아는 5차방정식의 근에 치환군으로 대수방정식의 제곱근이 존재하느냐이다. A60 교대군까지 내려온다. 조르당은 행렬로 바꾸어 선형변환을 연구했다. 리는 갈루아가 대수방정식 했던 것을 미분방정식의 해에 대한 그룹이론을 전개했다. 무한소 회전군 eε(d/dx)f(x)=m(x+ε)+b 가 되어 이동을 시켰다는 것이다. 무한소 회전 오퍼레이터를 연구하였다. 그래서 물질과 에너지와 시간에 대한 물리학이 결합이 되었다. 킬링은 갈루아가 5차방정식에 대해서 답이 120가지 조합으로 치환관점에서 테이블을 만든 근의 조합을 리가 미분방정식으로 그 일을 한 것을 킬링이 리가 한 분류를 봤더니 4가지 대칭군으로 요약됨을 보았다. 킬링의 4군이다. 그것이 SU(n), SO(2n), SO(2n+1), SP(2n)이다. n은 공간차원이다. 이 중 SO집합이 입자물리학으로 올라온 족보이다.
#8
UY(1)은 1차원 직선반사이고, SUL(2)는 원 회전 대칭군, SUC(3)는 구면대칭이다. 축구공이 있고(SO3), 동전을 붙이고(SO2) 바늘이 있는 것(SO1)이다. 직선과 동전과 축구공이 결합하 형태로 회전 변환이 일어난다는 것이다.
SO는 special orthogonal로 ‘특수직교함수’라고 하고, 수학자들이 쓰는 회전군이다. 물리학자들이 쓰는 SU는 Special Unitary group이다. 행렬을 구성요소로 하는 그룹이다. Unitary는 행렬의 dagger와 역행렬이 같은 행렬이다. 행렬값이 1인 것을 Special이라고 한다. Special Unitary 행렬이다.
SUL(2)×UY(1)를 해서 나온 값이 sin2Θw=0.23으로 ‘와인버그각’이라고 하는데 혼합각이다. SUL(2)×UY(1)가 섞여서 4개의 입자가 출현한다.
U(1)의 Local gauge symmetry 요청으로 나온 것이 γ(photon)이다. SU(2)의 Local gauge symmetry 요청으로 게이지 필드를 실어나르는 입자가 출현하는데, W+, W-, Z0이다. 단독으로는 안 되고 SUL(2)×UY(1)가 곱해지는 과정에서 출현한다. 이를 표준모형(Standard model)이라고 한다. 지금까지 계산한 내용이다. 우리나라 이휘소 박사를 포함한 많은 천재과학자들이 맹활약해서 마지막에 입자가속이게서 힉스입자를 찾아냈다.
Global gauge symmetry는 물리학의 계산이 아니다. 80억 인류를 모두 그 자리에서 동시에 한 바퀴 돌게 하면 차이를 알 수가 없다. 모든 구성요소가 동시에 치환하여 어떤 변화도 측정할 수 없기 때문이다. 이론상으로만 나오는 것이다. 물리학에서는 Local gauge symmetry 이다 변화를 알 수 있는 것은 축구공 한쪽이 찌그러드는 것이다. 그러면 어떻게 펴는가? 로칼로 대칭이 깨졌을 때 이것을 펴려면 4가지 힘이 필요하다. 힘을 실어나르기 위해 입자가 출현해야 한다. 힘을 실어나르는 입자를 보존(boson)이라고 한다. 대칭이 깨어지면 Local gauge symmetry를 맞추기 위해 보존이 출현하는데, 전자기장 U(1)에서 깨지면 포톤이 출현하고, 약력 SU(2)에서 깨지면 W+, W-, Z0 입자가 출현한다. SU(3)는 8가지 글루온이 출현한다.
입자가 출현할 필드가 있어야 하니, 처음에는 전자기장을 Bμ로 생각했다. Bμ에는 질량 m이 출현한다. 그런데 포톤은 질량이 없다. 마지막에는 Aμ가 나오는데 전자포텐셜 4벡터이다. 4차원 시공에 전자기현상을 담당하는 모든 정보를 갖고있는 4차원 벡터(A0, A->)이다. 3차원 버전에서는 A0는 전압(V)이 되고, A->는 전류가 된다. Current Jμ라고 적으면 이것도 4차원 물리학이다. Jμ=(J0, J->)로 적을 수 있고, J0는 전류의 시간에 대한 문제이므로, 쿨롱포스 ρ로 적게 된다. ∂μ=∂/∂xμ로 적고, 이는 (∂0, ∂1, ∂2, ∂3)=(∂0, -∇)가 된다. ∂μ∂μ를 계산하면, (∂0, ∂1, ∂2, ∂3).(∂0, -∂1, -∂2, -∂3)=∂0∂0-(∂1)2-(∂2)2-(∂3)2=∂0∂0-∇2이 된다. 4차원 시공의 시간성분과 공간성분을 한꺼번에 계산하기 위한 고차원적 수학기법이다.
#9
우리가 구한 w입자 질량은 “mw± = (1/2)g2 v” 에서 진공에너지(vaccum energy) v가 뭐냐? 진공에너지를 계산한다는 것은 우주론에서 어마어마하게 중요하다. 어떻게 계산할 수 있는가? 100년 이상 연구되었고 엄밀한 계산이다. 페르미(Enrico Fermi, 1901-1954)가 베터붕괴를 1930년대에 연구하면서 많은 실험을 통한 경험식이 있다.
페르미가 g2/8mw2=G/√2 라는 공식을 만들어 냈다. g는 커플링계수, G는 약한상호작용의 페르미상수로 1.17×10-5 GeV/C2 이다. 측정해서 안 값이다.
mw± = (1/2)g2 v에서 g=2mw/v 가 되므로, g를 위 공식에 넣으면,
(2mw/v)2/8mw2=G/√2 가 되고, 정리하면, 1/v2=G/√2 가 된다.
따라서 우리가 알고자 하는 진공에너지 v=1 / 2(1/4)√G =246GeV가 나온다.
양성자 250개 질량이다.
세상에! 충격받아야 한다. 우주의 모든 공간에 진공에서 가지고 있는 기본에너지가 246GeV라는 것이다. 어마어마한 에너지이다. 온도로 환산하면 조단위다.
전자 e=gsinΘw라고 하였다. 이것도 기겁할 일이다. sin2Θw=0.23 이라는 것을 측정해서 알게 되었다. 그러면 mw=(1/2)gv 이므로, 집어 넣을 수 있다. 우리는 e값을 알고, sinΘw값을 알고 있으므로, g값을 알 수 있다. 어마어마한 이야기이다.
따라서 mw=(1/2)gv=(1/2)(e/sinΘw)v=80 GeV 로 양성자의 80배이다.
불확정성원리 공식은 (∆x)(∆P)≥ħ/2 이고 에너지와 시간의 불확정도는 (∆E)(∆t)≥ħ/2 가 된다. 이 공식을 쓰면, W입자 질량이 양성자의 80배면 어마어마하게 무겁다. “운동량(∆P)=질량(m)×속도(v)”인데, 질량이 어마하게 커지면 ∆P가 어마하게 커진다. 그러면 ∆x는 무지하게 적어져야 하므로, W입자가 활동할 수 있는 영역이 무지하게 좁아진다는 말이다. 그것이 10-16m이다. 원자핵 크기가 10-15m이니 원자핵 사이즈의 1/10로 원자핵 속에서만 존재한다. 그래서 w입자를 아무도 본 사람이 없다. 원자핵 속에만 있기 때문이다. 가벼우면 멀리 간다. 질량이 0가 가장 가볍다. 그러면 영원히 우주 끝까지 가는데, 그것이 질량이 0인 광자이다. W입자는 양성자 질량의 80배가 되므로 원자핵 속에서만 중매를 선다. 이것을 조사하려면 원자핵 속을 들여다 봐야 한다. 그래서 원자핵 속까지 입자를 집어넣기 위해 어마어마한 가속에너지가 필요하고, 그래서 CERN에서 21km 지하터널을 만든 것이다.
Z 입자 질량은 mZ = (1/2)√(g12+g22) v 인데, 다른 공식은 mZ = mw/cosΘw 가 있다. Θw 각에 정보가 들어있으며 값을 안다. 그러면 mZ = 90GeV가 나온다. 이로써 W+, W-, Z0의 3개 입자의 질량을 끝까지 구하였다. 인류역사상 가장 큰 혁명을 일으켰다. 나머지 전자, Up-quak, down-quak 질량은 간단히 계산된다.
#10
여러분들이 알아야 하는 것은 라그랑지안이다. 입자물리학은 라그랑지안을 연구하는 학문이다. 라그랑지안은 에너지이다. 작용은 라그랑지안을 시간에 대해 적분한 것이다. 드브로이 물질파에서 파장 λ 은 단위가 ‘길이’이다. 그러면 계산 후에는 길이가 되어야 한다. 그래서 λ=h/P가 되어야 한다. h는 작용으로 ‘에너지×시간’이다. P는 ‘질량×속도’이다. 에너지는 mv2으로 적을 수 있고, P=mv를 나누어주면 v가 남고 여기에 시간을 곱하면 ‘길이’가 나온다. 물리량이 나오면 차원을 적어보면 알 수 있다. 작용인가, 에너지인가, 힘인가? 에너지는 스칼라이다. 힉스장은 스칼라장이다.
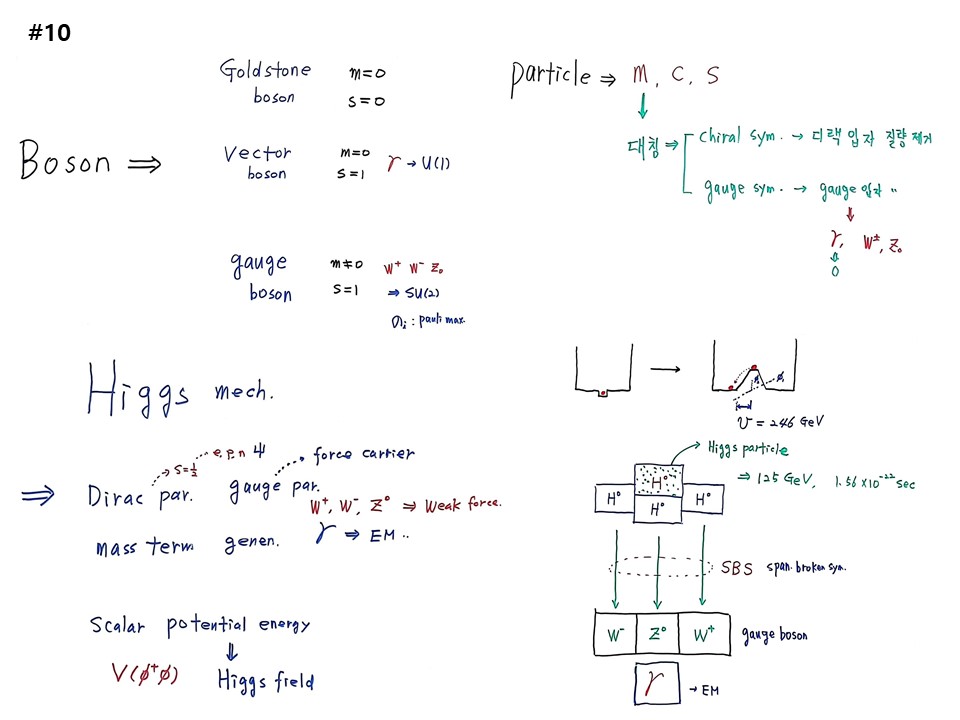
입자물리학에서 쓰는 스칼라량을 정리해 준다. 보존(Boson) 입자는 3가지 있다. 골드스톤 보존(Goldstone boson), 벡터 보존(Vector boson), 게이지 보존(Gauge boson)이다.
골드스톤 보존은 질량이 0, 스핀이 0이다. 그러므로 우주에서는 발견되지 않으므로 이론상만 있고 생기자마자 사라져야 한다. 벡터보존은 질량은 0인데, 스핀이 1이다. 대표적인 것이 포톤(γ)이다. 포톤 대신 고급과정에서는 벡터보존이라고 한다. 전자기상호작용을 매개해주는 광자이다. 질량이 0가 되는 것은 진공과 커플링했는데 0가 된 것이다. 그래서 힉스필드와 상호작용하지 않아 자유롭게 된 것이다. 게이지 보존은 질량은 0가 아니고, 스핀이 1이다. 질량을 획득한 것으로 W±, Z0이다. γ를 다루는 대칭이 U(1)이다. W±, Z0이를 다루는 대칭이 SU(2)이고, 이것의 제너레이터가 ‘파울리 매트릭스(σi)’로 공간상의 내부회전을 말한다.
모든 입자는 3가지로 구분한다. mass, charge, spin이다. mass의 웬수는 대칭이다. 질량과 대칭은 함께 존재할 수 없다. 대칭에서 chiral symmetry는 디랙입자 질량을 제거한다. gauge symmetry에서는 gauge 입자(γ, W±, Z0) 질량을 제거한다. γ 질량은 0이므로 제거가 되었다. W±, Z0는 질량이 출현했으므로, 질량을 획득하는 과정이 힉스메커니즘이다.
힉스메커니즘(Higgs mecanism)은 스칼라 포텐셜 에너지에 의해서 디랙입자와 게이지입자가 질량을 획득했다는 것인데, 디랙입자는 스핀이 1/2로 전자, 양성자. 중성자로 렙톤과 쿼크를 말한다. 디랙입자를 나타내는 파동함수를 Ψ로 적는다. 게이지입자는 force carrier로 W±, Z0는 약력을, γ는 전자기력을 매개해 준다. 우주를 구성하는 모든 입자의 질량을 스칼라 포텐셜 에너지가 만들어주었다는 이야기인데, 그 에너지가 V(∅†∅)이다. 스칼라포텐셜을 힉스필드라고 한다. 힉스필드장은 우주자체이다. 우리 우주에 있는 모든 별, 은하, 사람은 힉스장에 담겨 있다. 이것을 발견한 것이 입자물리학에 가장 큰 것이다.
힉스장은 양자요동한다. (∆E)(∆t)≥ħ/2 에서 시간(t)이 줄어들면 에너지(E)가 커진다. 시간이 찰나인 10-22초이면, 에너지가 어마하게 커져서 양성자 100배 정도가 되면서 입자가 생겨 난 것이다. 입자와 장은 분리된 개념이 아니고 모기장이 있는데, 눈금 하나가 올라오는 것이 입자이다. 우주를 가득 담고 있는 모기장이 ‘힉스장’이다. 힉스장에서 볼록 튀어나오는 입자가 ‘힉스입자’이다.
우리는 우주의 진공은 중심에 가장 낮은 포인트에 있는 줄 알았는데, 알고보니 바닥 중심이 최소가 아니게 볼록 올라와 있다. 가만 내버려 두면 바닥으로 떨어진다. 이것이 ‘힉스장’이다. 힉스장의 진공에너지 값 v는 볼록한 중심에서 떨어진 에너지로 246GeV이다.
다른 모식도로 그리면, 힉스장(H0)이 4개가 있으면, 힉스장 3개가 내려와서 질량을 획득하여 게이지보존입자 W-, Z0, W+로 바뀌어 약력(Weak force)이 된다. 그리고 이 과정에서 자유로운 입자가 출현한 것이 γ이고, 전자기상호작용(EM)이 된다. 남은 힉스장은 힉스입자가 되었는데, 에너지가 125GeV이고, 수명이 1.56×10-22초이다. 이 과정이 살람(Abdus Salam, 1926-1996)이 1979년 노벨상 받은 유명한 “자발적 대칭 붕괴(SBS, spontaneous broken symmetry)”이다. 원래 있던 진공에서 더 아래 진공으로 떨어지면서 나오는 125GeV 에너지로 모든 입자가 질량을 획득했다는 것이다. 그래서 우주가 출현했다. 이것이 인류가 발견한 최고의 지식이다.
#11
정리하면, 가장 아름다운 수식을 쓴다. SU(3)를 결합해야 하는데, 그 공식을 적는다. 모든 것은 운동에너지가 갖고 간다. 궁극적으로 입자물리학은 라그랑지안을 갖고 가는 이야기 밖에 없다. 라그랑지안은 나하고 우주에 관한 이야기이다. 나를 대표하는 에너지는 운동에너지이다. 먹이를 찾아서 내가 움직인다. 그런데 자연은 가만 있는다. 내가 어떻게 움직여야 하는가? 그것을 수식으로 표현한 것이 라그랑지안이다. 전자의 라그랑지안, 쿼크의 라그랑지안 인간의 라그랑지안 다 이야기 할 수 있다. “라그랑지안=운동에너지-위치에너지”이다. 그런데 이것을 계산하는 과정에서 이 모든 변화율을 누가 갖고 가는가? 자연은 쉽게 변화하지 않는다. 그래서 내가 바뀌어야 생존한다. 생물학과 같은 이야기이다. 나의 변화율 속에 우주의 모든 것을 담는다는 개념이 라그랑지안 철학이다. 운동에너지의 미분 속에 있다. 운동에너지는 mv2이다. v는 시간에 대한 거리의 한번 미분이다. v2은 두 번 미분이다. 그래서 L=(Dμ∅)†(Dμ∅) - V(∅†∅) 공식에서 (Dμ∅)†(Dμ∅) 텀은 두번 곱해져서 v2이 된 것이다. V(∅†∅) 텀은 위치함수이다. 산이 있으면 거리의 함수이다. 내가 어찌할 수 없다. 그런데 앞에 텀에서 내가 변하는 과정에서 뒤에 텀의 바뀌지 않은 자연에서 에너지를 준다는 것이다. 그 에너지가입자로 바뀐 것이 힉스메커니즘이다.
SU(3)까지 포함한 공식은 공변미분 Dμ에 모든 것을 담으면,
Dμ=∂μ+ig1(Y/2)Bμ+ig2(τ/2)Wμ+ig3(λ/2)Gμ 가 된다.
첫번째 텀 ∂μ는 4차원 시공의 편미분이다. 두 번째 텀 ig1(Y/2)Bμ에서 g는 커플링계수, Y는 photon에 대해 들어가는 hyper-charge, Bμ는 photon field로, 빛에 관한 모든 물리변화는 이 속에 다 들어간다. 세 번째 텀 ig2(τ/2)Wμ에 약한상호작용이 다 들어간다. τ는 공간의 회전자로 파울리 매트릭스(σi)가 되고, Wμ는 Weak field이다. 오늘은 여기까지 푼 것이고 스탠다드 모델이다. 여기에 쿼크까지 연결하면 3번째 텀 ig3(λ/2)Gμ로 강한상호작용까지 들어가서 중력을 빼고는 다 설명한다. 이 공식만 기억하면 된다.
Hyper-charge Y가 어디서 왔는가?
Q=I3+(Y/2)
이것이 유명한 “겔만-니시지마Gell-Mann–Nishijima)” 공식이다. 실험식으로 노밸상 받았다. I3는 isospin으로 I=(n-1)/2에서 왔다. n값은 다중항으로 양성자, 중성자 (p / n)을 묶거나, up-quark과 down-quark의 (u / d) 묶으면 이중항으로 n=2이다. (∑-, ∑0, ∑+)로 묶으면 3중항으로 n=3이다. 이렇게 단순하게 묶는 것이 중요해지는가? 처음에는 와 닿지 않는데 굉장히 중요하다.
Q=I3+(Y/2) 공식으로 up-quark과 down-quark의 (uL / dL)를 계산하면,
전하량(Q)은 2/3, -1/3이고, n=2이므로 I=1/2이 되므로 위에는 1/2, 아래에는 –1/2로 적는 것이 I3이다.
(uL / dL) = (2/3 / -1/3)= (1/2 / -1/2) + (Y/2 / Y/2) 가 된다. 그러면 Y값이 1/3가 나온다.
그런데, up-quark의 Right는 단일항이다. down-quak 이 없다. 전하량은 2/3이다. 단일항이므로 n=1이고 I=0이다. 그러면,
uR = (2/3) = 0 + (Y/2) 가 된다. 그러면 Y값이 4/3가 나온다.
Left up-quark의 Y값은 1/3, Right up-quark의 Y값은 3/4 라는 것은 굉장히 깊은 의미가 있다. UY(1)에서 Y는 멋으로 집어넣은 것이 아니다. U(1)을 따질 때는 Y값으로 모든 입자가 달라진다.
왜 포톤의 질량이 0인가를 이해하려면 포톤의 Y값이 1인가를 알아야한다.
이중항 ∅=(1/√2)(∅1 / ∅2)로 적으면,
이중항이므로 n=2를 넣으면, I=1/2이 되고, 전하량은 1, 0이다.
따라서 (1 / 0) = (1/2 / -1/2) + (Y/2 / Y/2)가 되므로, Y=1이 된다.
Y=1이 되기 때문에 포톤과 힉스장이 상호작용하지 않는다. 그래서 포톤의 질량이 0인 것을 이해할 수 있다. 모든 입자는 힉스장에 엉겨붙어 질량을 뜯어 오는데, 포톤은 Y=1이므로 힉스장과 상호작용 안 하기에 질량을 획득 못 하고 작용범위가 무한대까지 간다.

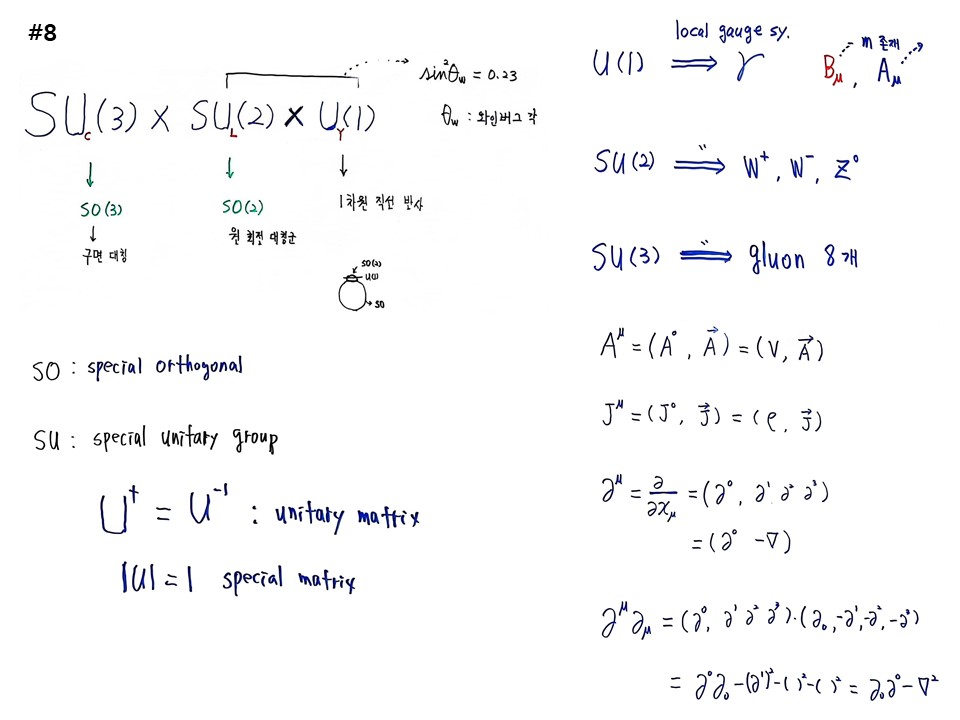
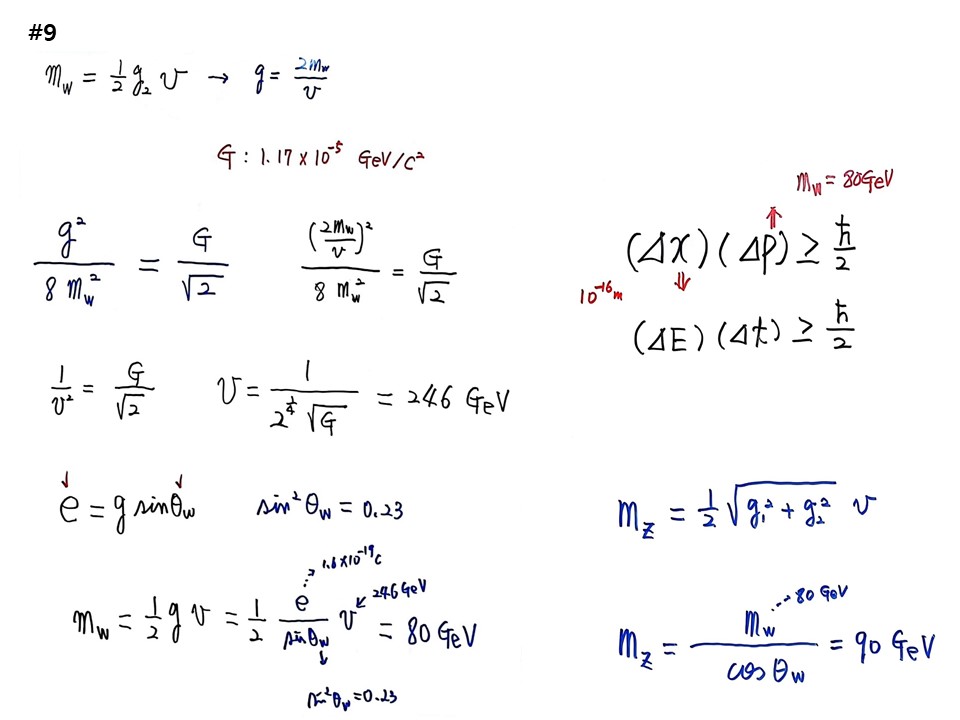

감사합니다!! 기다리고있었습니다! ^^