수업후기
#6
다음은 라그랑지안을 풀어야 한다. SUC(3)×SUL(2)×UY(1) 3개가 다 들어가는 라그랑지안이다.
L = Ψbar(γμ∂μ - m)Ψ + (g1/2)YΨbar(γμBμ)Ψ + (g2/2)Ψbarγμ(τWμ)Ψ + (g3/2)Ψbarγμ(λGμ)Ψ
입자물리학은 Ψbar( )Ψ를 푸는 것이다. 그래서 ΨbarΨ가 뭔지 알아야 한다. ΨbarΨ는 ’확률밀도‘이다. 양자역학에서 전자가 존재할 확률 Ψ*Ψ의 4차원 버전이다. ( )에 들어가는 양이 γμ가 되면 4차원 current Jμ가 되어 확률흐름이 된다. 우주의 모든 존재의 4차원 시공의 확률흐름을 계산한다. 전자가 흘러가는 확률흐름을 전류라고 한다. 어딴 사람이 살아가는 확률흐름을 추적하면 일생일대기가 된다.
첫 번째 텀은 Ψbar(γμ∂μ - m)Ψ 로 디락입자 fermion에 관한 이야기이다. Ψbar(γμ∂μ - m)Ψ 은 (γμ∂μ - m)의 4차원 시공의 확률흐름이다. γμ∂μ는 운동에너지, m은 위치에너지이므로 그 차이는 라그랑지안이 된다. 운동에너지와 위치에너지 차이에 해당되는 값이 4차원 시공에서 움직일 때 그 흐름의 확률값을 구한다는 것이다.
두 번째 텀은 (g1/2)YΨbar(γμBμ)Ψ 로 UY(1) photon에 관한 이야기이다. Bμ는 질량을 갖고 있는 빛으로 이론상 도입되는 양이다. 궁극적으로 나오는 것은 질량 0인 photon field Aμ이다. 전자기장의 4원 벡터이다. 여기서 전압과 전류가 나온다. Ψbar(γμBμ)Ψ는 γμBμ의 확률값을 구해보겠다는 것이다. 도대체 물리학이 궁극적으로 다루는 것이 뭔가 감을 잡아야 한다. 이 세상 모든 것을 4차원 시공의 확률흐름으로 본다. 거대한 우주의 시간과 공간의 강이다. 우리는 그 강에 흘러가는 이벤트 다발이다. 여러분과 나는 이벤트 다발을 동일한 시간상의 칼로 잘라서 같은 장소에 있게 된다. 저녁이 되면 뿔뿔이 다른 공간으로 흘러간다. Ψbar(γμBμ)Ψ은 이벤트 다발을 행렬로 만든 것이고 이벤트 다발을 잘랐을 때 드러나는 값이다. 어떻게 인간이 여기까지 상정하고 만들어냈는가 놀랍다. 자연과학의 최고 정수가 입자물리학이다.
세 번째 텀은 (g2/2)Ψbarγμ(τWμ)Ψ 로 SUL(2) weak force에 관한 이야기이다. Wμ에서 w+, w-가 나온다. UY(1)과 상호작용하는 과정에서 z0가 나온다. τ가 σ matrix (2×2)이다.
네 번째 텀은 (g3/2)Ψbarγμ(λGμ)Ψ 로 SUC(3) strong force에 관한 이야기이다. Gμi에서 i=1~8가지 있다. 이것이 8개 gluon이다. λ는 겔만 매트릭스로 2차원 σ matrix를 3차원(3×3)으로 확장한 것이다.
#7
메트릭스를 정리한다.
σ를 Pauli matrix라고 하고,
σ1=(0 1 /1 0), σ2=(0 -i /i 0), σ3=(1 0 /0 –1) 가 된다.
다음은 파울리 매트릭스를 3차원으로 확장한 것이 겔만 매트릭스 λi인데 i=1~8까지이다. 3×3 매트릭스로 8개이다.
λ1=(0 1 0 / 1 0 0 / 0 0 0) 인데, σ1이 포함된다.
λ2=(0 -i 0 / i 0 0 / 0 0 0) 인데, σ2이 포함된다.
λ3=(1 0 0 / 0 -1 0 / 0 0 0) 인데, σ3이 포함된다.
λ4=(0 0 1 / 0 0 0 / 1 0 0)
λ5=(0 0 -i / 0 0 0 / i 0 0)
λ6=(0 0 0 / 0 0 1 / 0 1 0)
λ7=(0 0 0 / 0 0 -i / 0 i 0)
λ8=(1/√3)(1 0 0 / 0 1 0 / 0 0 –2)
#8
SUL(2)×UY(1) 까지 푼 것이 표준모형이다. SUC(3)는 안 건드린다. 지금부터 입자물리학에서 quark을 다룰 때는 SUC(3)를 다루어야 한다.
SUL(2)를 다룰 때는 L의 Left Right를 다루는데 이것을 chirality라고 한다. Left, Right를 이해하는 것이 입자물리학의 30%이다. 이것이 γ 매트릭스에서 왔다.
그래서 PL=1/2(1-γ5), PR=1/2(1+γ5) 이다. P는 Parity이다.
γ5=iγ0γ1γ2γ3
γ5γ0=-γ0γ5
ΨbarPLΨ를 써서 이 함수 속에 Left Right 성질이 어떻게 들어가 있는지 보여줄 수 있다.
PLΨ=ΨL
PL+PR=1
P(Ψ)=γ0Ψ
P(Ψ)=γ0Ψ
P(Ψbarγμγ5Ψ)=Ψbarγ0γμγ5γ0Ψ=-Ψbarγ0γμγ0γ5Ψ
γμ는 axial vector JAμ가 되므로,
JA0를 Parity하면 -Ψbarγ0γ0γ0γ5Ψ 가 된다.
γ0γ0=1이 되므로
P(Ψbarγμγ5Ψ)=-Ψbarγ0γ0γ0γ5Ψ = -Ψbarγ0γ5Ψ 가 된다.
JA-k를 Parity하면 -Ψbarγ0γkγ0γ5Ψ 가 되고,
γ0γkγ0 = -γk 가 되므로
P(Ψbarγμγ5Ψ)=-Ψbarγ0γkγ0γ5Ψ = +Ψbarγkγ5Ψ 가 된다.
γ0는 시간성분, γk는 공간성분이다. 시간성분은 parity가 깨지는데, 공간성분은 parity가 안 깨진다. 그래서 Ψbarγμγ5Ψ 물리량은 parity가 깨진다. 그래서 약한상호작용에서 parity가 깨진다는 것으로 중국계 양전닝(楊振寧, 1922~ )과 리정다오(李政道, 1926~ )가 노벨상을 받았다.
#9
겔만이 노벨상 받은 하드론 10중항(decuplet).이다. 10개의 소립자도 쿼크 모델로 설명이 된다.
Q=2, Q=1, Q=0, Q=-1로 나뉘고, x축은 I3,로 I=(n-1)/2에서 4중항은 3/2이 되어 –3/2, -1, -1/2, 0, +1/2, +1, +3/2이 된다. y축은 strangeness로 0, -1, -2, -3으로 된다.
S=0인 4중항은 ∆-, ∆0, ∆+,∆++, S=-1인 ∑-, ∑0, ∑+, S=-2인 Ξ-, Ξ0, S=-3인 Ω-, 가 된다. 여기서 Ω-가 혁명을 일으켰는데, 그때까지는 발견이 안되었다. 도표를 만들고 선언을 하면서, 질량을 예측했다. ∆++질량이 1232 MeV로 측정을 했다. 다음 S가 많아질수록 150 MeV 차이가 난다는 것을 알았다. 그래서 ∑+, 질량은 1382 MeV, Ξ0는 1532 MeV가 되니, Ω-도 +150을 하면, 1682 MeV로 선언했다. 그랬더니 동료학자가 한 달 만에 찾아냈다. 답을 가르쳐 주니 바로 찾아내고 전세계 학자들이 이것은 틀릴 수 없다고 인정하였다. 그래서 1969년에 노벨상을 받게 된다.
Hadron decuplet으로 qqq가 오면 된다. 따라서 ∆++=uuu, ∆+=uud, ∆0=udd, ∆-=ddd 가 오면 된다. ∑-, ∑0, ∑+,와 Ξ-, Ξ0, 하드론 8중항에서 다 했다. Ω-=sss이다.
#10
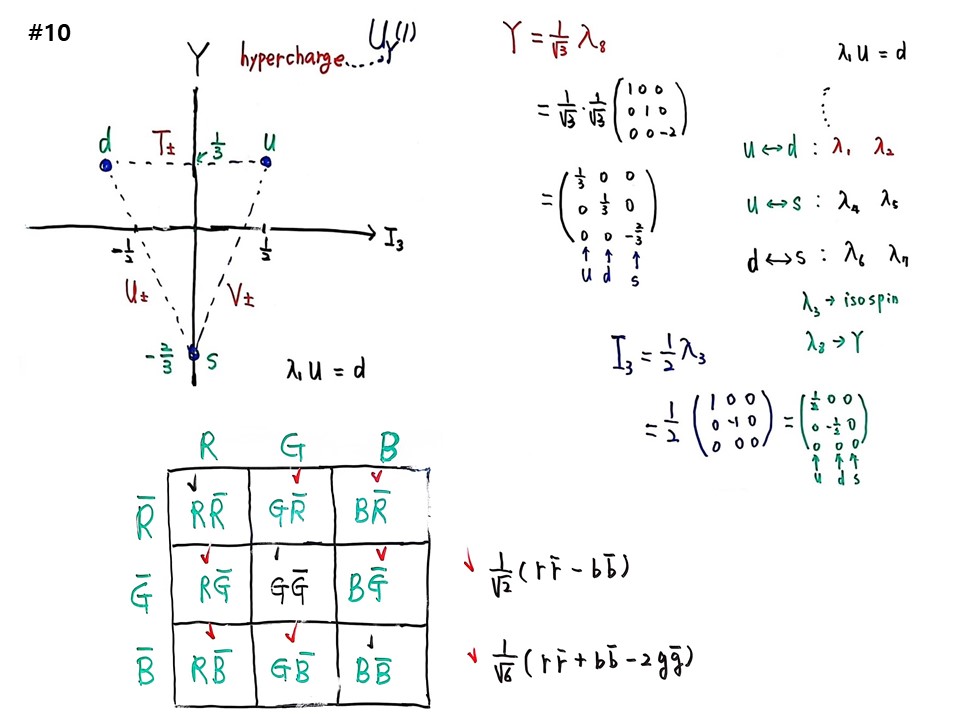
Strangeness S=B+Y 임이 밝혀지고, 이 모델이 왜 이렇게 잘 맞는지 관계를 알게 된다. hypercharge Y값은 s=-2/3, u=d=1/3이다. I3값은 u=1/2, d=-1/2, s=0이다.
Y=(1/√3)λ8 가 됨이 밝혀졌다.
=(1/√3)(1/√3)(1 0 0 / 0 1 0 / 0 0 –2)
=(1/3 0 0 / 0 1/3 0 / 0 0 –2/3) 가 되어
s=-2/3, u=d=1/3 Y값이 여기서 나온다.
겔만매트릭스 8번째와 Y값이 링크되어 있다는 것이다.
I3=(1/2)λ3 가 됨이 밝혀졌다.
=(1/2)(1 0 0 / 0 -1 0 / 0 0 0)
=(1/2 0 0 / 0 –1/2 0 / 0 0 0)
그래서 I3값은 u=1/2, d=-1/2, s=0이다.
Y와 I3의 계산값이 어디와 링크되어 있는지를 봤더니 겔만 매트릭스와 링크가 되었다. 겔만매트릭스 Gμ는 라그랑지안의 SUC(3) 텀인 (g3/2)Ψbarγμ(λGμ)Ψ 에 들어있다. 그래서 겔만 매트릭스가 글루온의 제너레이터가 된다. 그래서 8종류의 글루온이 출현한다.
u와 d의 치환이 가능한 것은 λ1과 λ2 매트릭스와 관계된다. 계산해보면 λ1u=d가 됨을 알 수 있다. u와 s의 치환이 가능한 것은 λ4과 λ5 매트릭스와 관계된다. d와 s의 치환이 가능한 것은 λ6과 λ7 매트릭스와 관계된다. 여기서 λ3와 λ8이 빠져 있는데, λ3는 Isospin과 관계되고, λ8은 Y값과 관계된다. 드디어 겔만 매트릭스 Gμ를 통해서 비밀이 다 밝혀졌다.
SU(3)에서 3은 2의 3승에서 왔다. 23=8이므로, 글루온이 8개 있다는 말이다. 글루온 8개를 제너레이션 하는 매트릭스가 겔만 매트릭스이다. 글루온 8개를 제너레이션 했기에, 글루온과 쿼크가 interaction해서 에너지 97%를 다 쓴다. 글루온과 쿼크가 어떻게 interaction 하는가가 겔만 매트릭스이다.
γ매트릭스 γμ, 파울리매트릭스 τ, 겔만매트릭스 Gμ 3가지가 어디에 들어가 있는가?
L = Ψbar(γμ∂μ - m)Ψ + (g1/2)YΨbar(γμBμ)Ψ + (g2/2)Ψbarγμ(τWμ)Ψ + (g3/2)Ψbarγμ(λGμ)Ψ
이 식에 다 들어있다.
작동하는 글루온은 색깔이 있다는 것이다. 그러나 RRbar, BBbar, GGbar는 색깔이 없으므로 작동 안한다. 테이블에서 작동하는 글루온은 6개이므로,
나머지 2개는 (1/√2)(rrbar-bbbar)와 (1/√6)(rrbar+bbbar-2ggbar)가 작동하는 글루온이다.
u와 d를 치환해주는 행렬 T±=(λ1±iλ2)가 된다. 더하기 빼기 밖에 앖는데 다 맞아 들어간다. 따라오려면 이해하려 하지 말고 암기를 해야 한다. σ matrix, γ matrix, Gelmann matrix,를 암기한다. σ matrix는 디락방정식에서 왔다. γ matrix,는 σ matrix를 4차원으로 확장한 것이다. 3차원으로 학장한 것이 Gelmann matrix,이다. 그래서 알아야 할 것은 σ matrix이다. 이것이 왜 이렇게 작동하는가? 대각선 매트릭스로 더하면 다 0가 된다. Traceless라고 한다. 그래서 모든 2차원 공간의 복소수를 이 3개의 매트릭스로 다 표현할 수 있다. 놀라운 이야기이다. 2차원 공간의 회전이다.
#11
수학사 중 리(Lie)에서 ’무한소 회전‘이라는 말이 나왔다. 모든 것이 회전이고 회전이 곧 행렬이다. 4차원 시공에서 회전이다. 상상할 수 없는데 수학적으로 증명한다. 방사회전이므로 원을 말한다. 원은 존재하지 않는다. 허수를 곱해주면 수직축으로 바뀌어지는 것이다. 4차원
시공에서 ’무한소 회전‘이고 모든 물리량이 다 나온다. 미분도 할 필요 없다. 지난 시간 미분이 행렬이라고 했다. 이 모든 것이 행렬로 다 모아졌다. 행렬과 자연상수는 어떻게 결합되는가? 다시 모든 문제는 e로 온다.
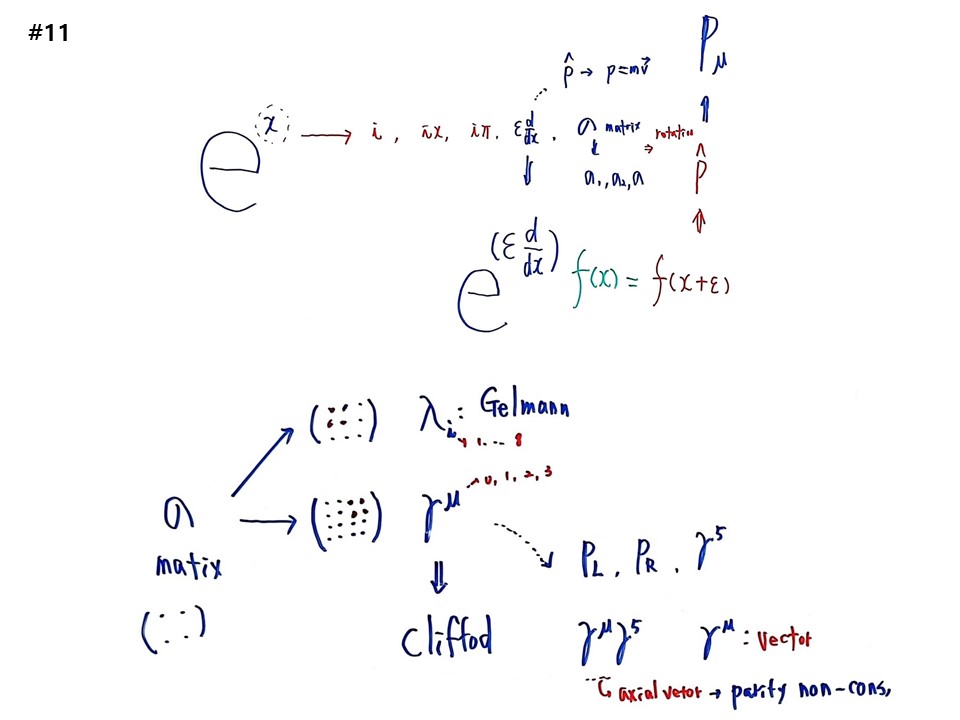
ex에서 x에 무엇을 집어 넣는가? Ii ix, iπ, ε(d/dx)를 넣는다.
x-> ε(d/dx)를 넣고 임의의 함수f(x)를 곱하면 f(x+ε)로 평행이동, 무한소 이동이 되고, 모멘텀 오퍼레이터 P가 되어 공간대칭이 된다. 이것이 디락방정식 (γμPμ-mc)Ψ=0 에 Pμ로 들어가 있다. P=mv와 연결된다.
x-> σ matrix를 넣으면, 입자물리학 계산이 된다. σ가 들어가면 회전(rotation)이 된다. quark 사이의 치환이 회전이다. up quark이 down quark으로 바뀐다. 이 모든 것이 일어나는 것이 σ matrix를 ex에 넣었기 때문이다. 이를 제너레이터라고 한다. 파울리매트릭스 σ를 SU(2)의 제너레이터라고 한다. 겔만매트릭스 λ는 SU(3)의 제너레이터이다 매트릭스 세계로 다 설명하겠다는 것이다.
입자물리학은 매트릭스 이야기이다. 첫 번째 2×2 σ matrix이다. σ matrix를 3×3로 확장한 것이 λi matrix로 i=1~8이다. 4×4로 확장한 것이 γμ matrix로 μ=0.1,2,3이다. γμ matrix의 대수를 ’클리포드 대수(clifford algebra)‘라고 한다. γμ matrix에서 파생되는 것이 PL, PR, γ5 오퍼레이터가 있고, γμ만 있으면 vector라고 한다. γμγ5로 된 것을 axial vector라고 하고, 이것은 parity non-conserved이다. 여기서 parity가 깨지는 것을 알고 중성류 비밀까지 연결되면서 거울상의 세계와 다르다는 것을 알게 되었다. Weak force가 깨진 것으로 양전닝과 리정다오가 노벨상을 받으면서 어마어마한 혁명을 일으킨다. 입자물리학에서는 오른쪽, 왼쪽이 완전히 다른 세계라는 것을 알게 된 것이다. 뉴트리노는 오른쪽 뉴트리노가 없다. 그래서 전부 구분해주어야 하는데, 구분해주는 오퍼레이터가 PL, PR 오퍼레이터이다.
이것을 다 알려면 γμ matrix 수학을 따로 해야 한다. γμ matrix는 디락방정식에서 왔다. 명확한 물리적 실체가 있다. 디락방정식은 슈뢰딩거방정식의 상대론적 버전이다. 그래서 다 설명하게 된다. 디락방정식에서부터 입자물리학이 시작되는 이유는 γμ matrix가 들어있어서이다. γμ matrix를 통해 표준모형(standard model)이 완성이 된다.

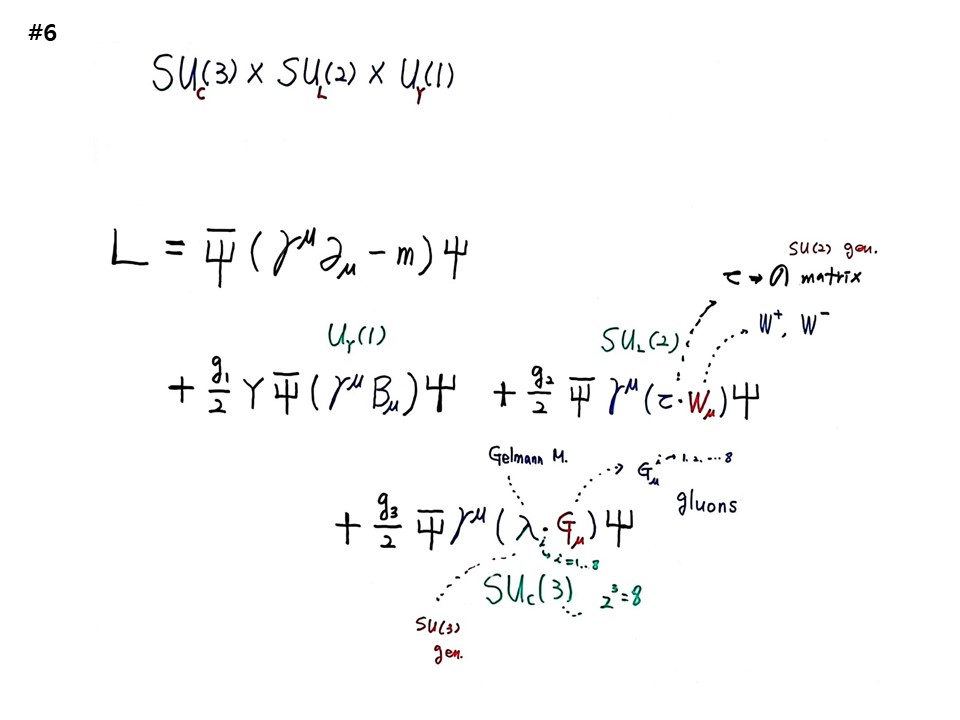
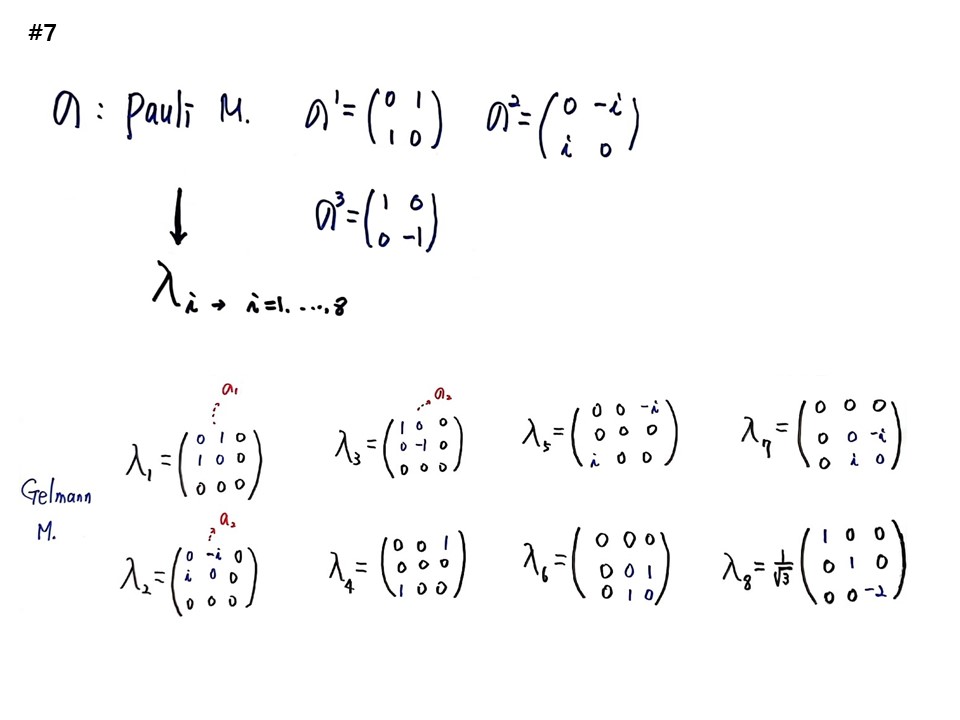


감사합니다~! 저도 5강 복습시작합니다!