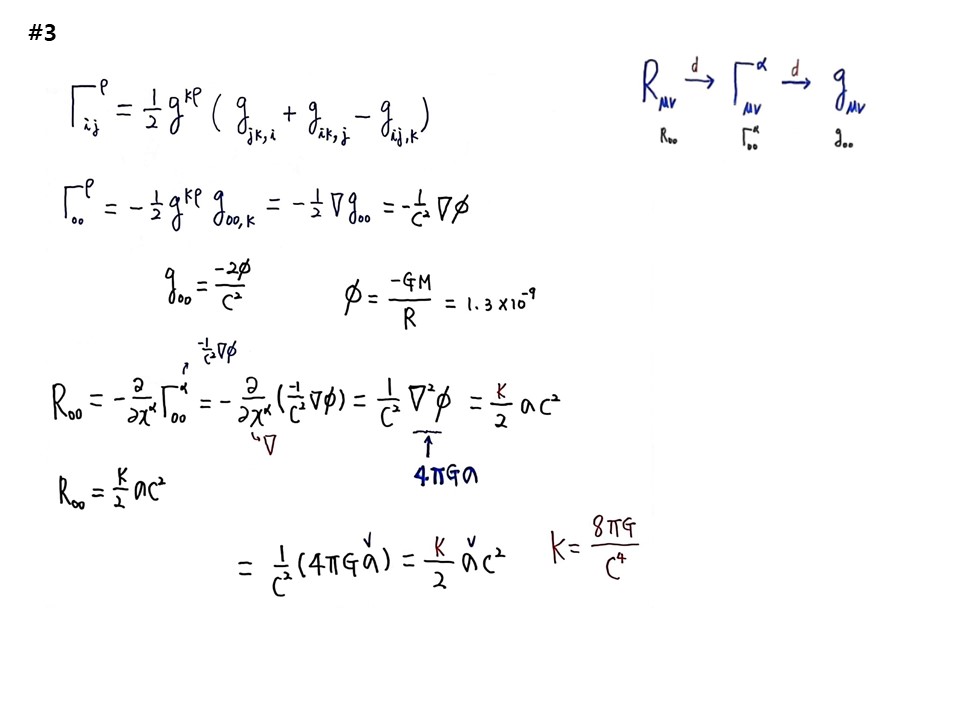수업후기
#0
E2=(pC)2+(m0C2)2은 15년째 강의에서 물리학에서 가장 기억에 남을 방정식 7-8개 중 entry number 2번, 3번에 해당되는 방정식이다. 이 공식 유도나 암기를 못하면 물리학을 모른다고 생각할 정도이다. 이 공식 암기하면 E=mC2은 암기할 필요 없다. 정지질량에서는 운동량이 0이다. 그래서 p=0로 두면 E=mC2이 나온다. E=mC2은 이 공식의 특별한 경우이다. 정지해 있을 때이다. 물질은 속도가 0이고, 빛은 질량이 0이다. 따라서 빛은 E=pC이 된다. 응용면에서는 E=pC를 더 많이 쓴다. 모든 빛은 E=pC부터 시작한다.
유도하는 과정까지 반드시 해야 한다. 4차원 세계에 들어가기 위해서는 키가 3개이다. 문이 3중으로 되어있어 아무리 몸부림쳐도 들어갈 수 없다. 4원 위치벡터로 첫 번째 문을 열고, 4원 속도벡터로 두 번째 문을, 4원 운동량 벡터로 마지막 문을 열면, 그 세계가 4차원 시공이다. 4원 운동량 벡터에서 곧장 E2=(pC)2+(m0C2)2이 나온다. 입자물리학이 여기서 시작한다. 특수상대성, 4차원 세계 3개의 키가 모두 달려있다.
t=τ/√1-(v/c)2 은 특수상대성 공식 3개 중 하나이다. 반드시 해야 한다.
v=Hr 허블법칙이다. 이것을 알아야 허불망원경, 제임스웹 망원경이 어떻고 할 자격이 된다. 갤럭시가 어떻고 우주가 어떻고 하는 ABC이다. 우주의 팽창속도(v)는 허블상수(H)에 비례하고, 반지름(r)은 우리를 중심으로 멀어지는 거리이다. 갤럭시가 멀리 있을수록 더 빠른 속도로 멀어진다. 풍선에 싸인펜으로 점을 찍어 불면 갤럭시 사이가 늘어나는데, 멀리 있는 쪽은 더 멀리 늘어난다. 갤럭시는 1000억개 별이 있는데, 갤럭시 속의 별과 별 사이도 늘어나는가? 틀렸다. 우주가 늘어난다 했을 때, 갤럭시 내에서의 공간, 지구와 태양 사이의 공간도 늘어날 것이라고 가르쳤는데 틀린 개념이다. 우주가 팽창했다는 것은 갤럭시를 구성하는 별 사이가 늘어난 것이 아니다. 갤럭시와 갤럭시 사이의 어마어마한 공간이 늘어난 것이다. 왜 갤럭시 내 별들 사이는 늘어나지 않는가? 별들이 서로 당기는 만유인력이 크기 때문에 늘어나지 않는다. 지금은 고무풍선에 싸인펜이 아니라, 동전을 갖다 붙인 것으로 설명한다.
허블법칙이 왜 중요한가? 천문학의 역사는 허블상수를 잰 역사이다. 허블상수의 역수가 바로 우주의 나이가 된다. 우주가 선형적으로 팽창하면 금방 알 것이다. 그런데 우주는 그렇게 팽창하지 않았다. 상수라고 하지만 허블상수는 계속 바뀐다. 우주의 시간(t)에서 반지름(r)이 RDU에서는 t1/2로 자라고, MDU에서는 t2/3로 자라고, ⋀DU에서는 e-H0√Ω 로 자란다. 우주팽창율이 허블상수이므로 그 속에 천문학의 구조가 다 들어가 있다.
단순한 키워드를 기억하라. 키워드를 기억하지 않은 사람들의 특징이 잡다한 자료 올리고, 잡다한 데 분산하고, 엉뚱한 소리하고, 아는 척한다. “허블상수가 뭔가?” 물으면 “허블상수 역수가 우주의 나이다”고 간단히 대답해야 한다. 우주의 나이 재는 것이 어마어마한 사건이다. 허블상수를 알게 되면서 우주의 나이가 137억년이라는 것을 알게 되었다. 누가 측정했는가? WMAP, PLANC 인공위성이 측정하면서 2002년부터 명확해지기 시작했다. 모두 허블상수와 링크된다.
P=wρC2 공식은 10개의 공식에는 들어기지 않지만, 우주론에는 반드시 알아야 한다. w값은 v2/C2 비와 관계있다. 보통물질의 MDU에서는 광속이 워낙 크므로 0가 된다. RDU에서는 1/3이 된다.
RDU에서 우주의 반지름 R은 √t에 비례하는데, 우주의 온도 T=1.5×1010(1/√t) 관계가 된다. 이것 하나만 제대로 응용하면 초기우주를 아는 것이다. 온도는 절대온도이다. 시간을 집어 넣으면 온도가 나온다. 100만분의 1초, 10-6을 넣으면 T=10-13이 된다. E=kT에서 볼츠만상수 k=8.6×10-5이므로, 10-4으로 봐도 되기에, T에 10-4 을 곱해주면 eV로 바뀐다. 왜 eV로 바꾸려고 할까? 시간을 10-6을 넣어서 eV로 바꾸는 이유가 있다. 뭘 이야기하고 싶은 것일까? ‘양성자’이다. 양성자가 뭔지는 이 공식이 아니면 설명할 길이 없다. 양성자 질량이 1GeV이다. 10-6초에서 10-9eV = 1GeV이다. 그래서 우주의 시간이 100만분의 1초가 되면 1GeV 온도가 된다는 말이다. 매번 강의 때마다 강조하는 얘기다. 이것만 깨달으면 4시간 버티는 이유가 된다. 양성자가 생물학, 지구과학에 어마어마하게 중요한데, 양성자의 기원을 얘기하는 것이다. 양성자 질량이 eV로 표시되었기에, 온도를 eV로 표시해야 양성자를 γ선이 만들 수 있는지 없는지를 가늠할 수 있기 때문이다. 양성자 온도는 11조 도이다. 전자의 질량 0.51 MeV를 온도로 바꾸면 59억도이다. 59억×2000=11조이다. 전자질량의 2000배가 양성자이기 때문이다. 중성미자는 1초를 넣으면 106 eV가 되어 1 MeV가 될 때 분리되어 나온다.
KB=8.6×10-5eV/T 볼츠만 상수이다. E=KT이다. 어떠한 에너지 준위에 입자가 들어갈 확률이 P(E)=e-βE인데, 에너지의 평균값<E>은 ∫0∞Ee-βEdE 해주면, <E>=KT값이 나온다. 온도의 정의가 여기서 시작된다. KB=8.6×10-5 이므로 대략 10-4가 되고, 온도 1만도(104)를 넣어주면 1 eV가 나온다.
어마어마하게 중요한 것을 했는데, T=1.5×1010(1/√t) 라고 적고 우주론이라고 읽으면 된다. 우주에 이거밖에 없다. 사고실험을 해 본다. 사람이 아프면 체온을 잰다. 지금 30도니 견딜 만하다. 40도가 되도 버틸 수 있다. 50도 올리면 인간은 4-5시간 못 버틴다. 60도 올리면 1시간 지나면 위험해진다. 70도가 되면 죽는다. 세포에 단백질 10만 종에서 효소작용을 못하기 때문이다. 20도 내려가도 효소작용 못한다. 그래서 생존온도가 20-40도 이다. 100도 넘어가도 사는 호열균 박테리아가 있다. 500도면 납이 녹는다. 1000도이면 지구표면이 녹는다. 마그마 온도가 900-1200도이다. 1500도면 웬만한 금속은 다 녹는다. 3300도면 텅스텐이 녹는다. 3500도면 다이아몬드가 녹는다. 그 외에는 지구상에 없다. 지구 내부는 5000도이다. 지구는 날고 기어도 5000도 이상이 없다. 5000도가 되면 지구는 모두 증기가 된다. 지구초기가 그랬다. 5000도가 되면 철이다 다이아몬드다 구분이 없다. 모두 기체가 된다. 1만도가 되면 전자가 떨어져 나가 모두 원자상태가 된다. 아직 별에는 근처도 못 갔다. 별로 들어가면 최소 1천만도가 되어야 한다. 1천만도가 되면 양성자, 전자 모두 분리된 플라즈마 상태가 된다. 그래도 원자 속은 들어갈 수 없다. 원자핵의 양성자로 들어가려면 1 GeV가 되어야 하고, 1013도가 되어야 한다.
물리 모든 변화를 무엇으로 얘기하는가? 온도가 낮을 때는 사람이 있고, 꽃이 있고 돌이 있고 강이 있다고 얘기하지만, 그 상에 속지마라는 것이다. 온도 하나로 물리학은 끝난다. eV로 바꾸는 것은 입자로 들어갈 때는 온도를 얘기하지 않는다. 입자는 eV로 따져준다. 우주론은 곧 입자물리학이다. 천체물리학에서는 온도가 들어가지만 입자물리학에서는 eV를 얘기한다. 거시세계는 온도로 얘기한다. 온도(T), 압력(P), 부피(V)로 드러난 세계가 거시세계이다. 미시세계는 아보가드로 숫자로 들어가고, 분자, 원자로 들어갈 때는 eV로 바꾸어야 한다. eV는 극대세계와 극미세계를 다 포함한다. eV로 바꿀 때는 10-4 곱해주면 된다. 100만분의 1초일 때 1013 k가 되고, eV로 바꾸면 109 eV가 되어 1 GeV라고 한다. 이것이 바로 양성자 질량에 해당된다. CMB는 우주초기의 광자이다. 이때가 RDU이다. 전자, 양성자가 1개면, 포톤은 10억개가 있었다. 지금은 CMB 에너지가 10-4eV이다. 빅뱅 당시는 1037K가 되었다. 그 공식이 T=1.5×1010(1/√t) 이다. 이 공식을 ‘우주론’이라고 읽는다.
#1
아인슈타인이 중력장방정식을 10년간 유도했는데, “힐버트-아인슈타인 텐서”라고 한다. 지금부터 30분 동안 다시 한번 해 본다. 오늘 강의를 이해하면 아인슈타인이 뉴턴 어깨에 올라가 있다는 말을 이해한다. 일단 어려운 부분이다. 오늘 하는 것은 물리가 있어서 이해를 반드시 해야 한다. 아인슈타인이 마지막에 정신이 분열될 정도로 올인하였다. 수학이 어려워 10년간 헤맸는데, 그것을 조금만 맛보면 된다. 힐버트는 100% 수학자이고, 아인슈타인은 90% 물리학자이고 수학은 10%이다. 수학에 대해서는 힐버트보다 수준이 낮다. 거의 10년간 아인슈타인이 독자적으로 밀어붙인 것은 자기가 방정식을 만든 것을 최종적으로 4차원 시공에 맞는 뉴턴역학을 접목시키는 것이다. 중력장방정식이 맞다는 것을 증명하려면 뉴턴방정식과 만나는 것을 보여주어야 한다. 아인슈타인이 다 해 놓고 맞는지 안 맞는지를 엄청 고민했다. 1915년 공식을 완성할 때쯤, 독일의 천문학회 모임에 가서 수성의 근일점 문제가 해결 안 되었다는 이야기를 듣는다. 그날 밤 공식에 수성의 근일점 문제를 넣었더니 57초가 계산되어 나왔다. 아인슈타인이 “유레카” 하면서 뛰쳐 나와서 “나는 신하고 직접 통한다”고 하면서 엄청 좋아하고 확신을 갖게 된다. 공식이 발표되고 인류역사상 가장 큰 지적혁명을 맞이한다. 우리는 4차원 시공에 살게 되었고, 뉴턴역학은 끝나고 아인슈타인의 4차원 시공의 역학, 중력장방정식의 세계가 도래한다. 아인슈타인이 궁극적으로 뉴턴방정식과 맞다는 것을 보여준 것이다.
일반상대성을 이해했느냐를 판가름하는 것이 비례상수 K값이다. 아인슈타인이 K값 8πG/C4를 처음 알았던 것이 아니다. 유도가 굉장히 어렵다. 고전물리학과 상대성이론을 모두 알아야 한다. 우주에 물질, 태양이 있다면, 화성, 금성이 돌아가는 것을 설명하고 싶었던 것이다. 뉴턴과 같은 것이다. 다른 것은 뉴턴은 만유인력이 당겨서 돌아간다고 하였지만, 아인슈타인은 4차원으로 이야기하려고 한 것이다. 만유인력에는 시간이 없지만 4차원에는 시간이 있다. 뉴턴이 했던 태양계 모델을 4차원 버전으로 바꾸어 놓고 싶은 것이다.
뉴턴이 만든 만유인력 공식은 GMm/r2 이다. 아인슈타인은 4차원으로 바꾸니, 물질에너지를 Tμν 매트릭스 값으로 두자고 했다. 뉴턴은 만유인력 공식에 상수를 집어넣은 것이고, 아인슈타인은 시간과 공간을 16개 요소로 집어넣은 것이다. 이것을 물질에너지 텐서라고 한다. 그리고 물질에 의해서 시공이 휘어졌다고 하고, 그것을 표현한 것이 Rμν이고, (Rμν-1/2gμνR)이 시공의 곡률이다. 시공이 휘어진 것이 침대에 당구공을 올려놓으면 휘어지는 것이다. 그 관계를 비례상수 K로 두었다. 처음에 Rμν를 곡률로 했다가 발산이 0가 아니므로 보존량이 아니기에 에너지보존의 법칙이 안되어 엄청나게 노력해서 (Rμν-1/2gμνR)을 유도해 낸 것이다. (Rμν-1/2gμνR)이 텐서인데, 공변미분해서 0가 되는 것을 보여준다. 그것이 비앙키항등식(Bianchi identities)이고 축약하면 이 공식이 나온다. 그래서 이 공식이 물리학방정식에 쓸 수 있는 텐서량이라는 것을 알게 된 것이다. (Rμν-1/2gμνR)를 부르는 이름이 Gμν 아인슈타인 텐서이다. Rμν는 리치텐서이다. 그 차이는 어마어마한다. 두 번째는 비례상수 K를 공략했다.
얼마나 아름다운가 느껴보라. 중력장방정식을 적어본다.
Rμν-1/2gμνR=KTμν 반드시 암기한다. Rμν-1/2gμνR=KTμν 로 적어도 된다.
μ, ν = 0, 1, 2, 3이고, 0은 시간(t), 1, 2, 3은 공간으로 x, y, z 또는 구좌표계에 r, Θ, Φ 로 적는다.
gμν를 곱해주면,
gμνRμν-1/2gμνgμνR=KgμνTμν 가 되고,
gμνRμν는 스칼라곡률로 상수 R이 되고, gμνgμν=4가 되고, gμνTμν=T가 된다.
따라서 R-2R=KT 가 되어, R=-KT가 된다. 이 관계를 기억해야 한다.
Roo 시간성분을 구해보면,
R00-(1/2)g00R=KT00 에서, R=-KT가 되므로,
R00=-(1/2)Kg00T+KT00 = (k/2)(-g00T+2T00)
g00T=T00 가 되므로,
R00=(k/2)T00가 된다.
비례상수 K를 구하는 과정이 놀랍게도 아인슈타인이 유도한 이 방정식을 푸는 과정이다. 뉴턴역학과 만나면서 물리학 전체를 알게 된다.
R00=(k/2)T00가 됨을 알고,
T00=σC2이므로 R00=(k/2)σC2이 된다.
시공의 곡률의 시간성분으로, 밀도σ에 광속도를 곱해준다.
리치텐서의 일반공식은
Rμν = ∂ν⌈αμα - ∂α⌈αμν + ⌈αμβ⌈βνα - ⌈ανβ⌈βμα
아인슈타인이 이 공식을 유도하고, 이 양이 에너지가 보존되는가를 공변미분하여 따져보니 0가 되지 않았다. 그래서 몸부림쳐서 비앙키항등식으로 들어가서 줄여서 아인슈타인텐서를 만들었다.
Roo 를 넣으면, μν가 모두 있는 두번째 항만 0가 안되고 나머지는 항은 0가 된다.
Roo = -∂α⌈α00 = -(∂/∂xα)⌈α00
다음은 ⌈α00 값을 알아야 한다. 그래서 측지선방정식을 푼다.
(duμ/ds) + ⌈ijμ(uiuj) = 0
4원속도벡터 uμ=dxμ/ds 로 들어가본다.
따라서 uμ에 집어 넣으면
(d/ds)(dxμ/ds) + ⌈ijμ(dxi/ds)(dxj/ds) = 0
ij에 00를 넣고 조작을 하면,
〔(d2xμ)/(dx0)2〕(dx0/ds)2 + ⌈00μ(dx0/ds)2 = 0
그러면 (dx0/ds)2를 없엘 수 있다.
dx0=cdt 이므로,
(d2xμ)/(Cdt)2 + ⌈00μ = 0
(d2xμ)/dt2 = -C2⌈00μ
(d2xμ)/dt2 는 F=ma에서 가속도 a이다. 포텐셜은 ke2/r은 전자기포텐셜, ke2/r2은 전자기력이 된다. 따라서 가속도 a이므로 Force이다. 포텐셜에너지를 미분하면 Force가 나온다. 포텐셜을 Φ로 두면 미분은 ▽Φ로 두면 된다. 여기서 점프가 일어난다. 뉴턴과 아인슈타인이 만나는 접점이다.
궁극적으로 K를 찾아내려는 것이다. 중력장방정식의 R00를 구한 것과 리체텐서의 R00를 구한 것을 비교하는데, ⌈α00 이 나와서 이 값을 알려고 측지선방정식을 물고 늘어진 것이다. 측지선방정식에 00텀을 넣어보니 가속도 형태가 나왔고, 가속도는 Force이므로 포텐셜에너지 Φ을 미분한 것 ▽Φ 과 같다고 둘 수 있다. 따라서 점프를 하여,
(d2xμ)/dt2 = -C2⌈00μ = ▽Φ 로 두고,
⌈00μ = -(1/C2)▽Φ 로 구했다.
#2
Φ는 ‘중력포텐셜에너지’이다. 중력포텐셜이 어떻게 주어지는지 보는 것이 큰 덩어리이다. 중력포텐셜은 뉴턴이 연구했다. 뉴턴의 중력이론을 필드이론으로 바꾼 것이 푸와송이다. 푸와송방정식을 유도할 수 있어야 한다. 고전물리학이다.
F->=ma-> = mg->이다.
앞에 m은 관성질량, 뒤에 m은 중력질량이다. 관성질량과 중력질량이 같다는 것이 중요한 등가원리이다. g는 중력가속도이다. 벡터이다.
g->=F->/m, 이때 F는 만유인력이다.
물리학은 몇가지 없다. 스칼라, 벡터, 텐서 3가지이다. Force는 벡터이다. 벡터의 에센스가 Force이다. “만유인력은 Force이니 벡터다”가 바로 나와야 한다. 벡터는 화살표로 표시한다. 만유인력은 Force이니 분모가 r2이다. 스칼라의 경우는 r이 된다. 이것 헷갈리면 물리학 못한다. Force는 r2이고, 에너지는 r이다. 미분적분 관계이다. 중력은 force이고 중력포텐셜은 에너지이다. 중력포텐셜의 에너지 바다에서 일어나는 파도 하나가 Force이다. 중력장방정식은 Force가 아니고 Field이다.
F->=-GMm/r2 이다.
이때 m은 test질량이다. 지구가 M이면 m은 달, 사람, 사과, 태양이 M이면 m은 지구이다. 벡터로 만들어주기 위해 중심방향으로 가는 unit vector r∧를 붙여주어
F->=(GMm/r2)r∧ 이 되고,
지구의 중력가속도 g->=-(GM/r2)r∧ 이 된다.
g->는 Force이다. 중력장방정식은 Field이다. 아인슈타인이 어깨에 올라간 거인 뉴턴의 중력장방정식을 푸와송이 만들었는데, 이것이 푸와송방정식 ▽2Φ=4πGσ 이다. 이때 Φ가 지구의 중력장이다. 이 공식을 유도하는 과정이다.
모든 벡터에 적용되는 공식이, 어떤 벡터 g의 축구공 껍질에 대한 적분과 축구공 껍질 속의 발산을 체적에 대해 적분한 것이 같다는 가우스법칙이다.
∫s g->ds-> = ∫v▽.g->dv
∫ g->ds-> = ∫ -(GM/r2)r∧ds-> 이 된다.
이 이야기는 축구공에 물을 넣고 누르면 구멍으로 물이 나오는 것을 divergence라고 하고 ▽로 표시한다. 벡터 g->로 표시하면, ▽.g->로 표시된다. 축구공 껍질에서 눌러서 물이 나오는 것은 반지름 r벡터 형태로 나오고, 물이 나오는 표면의 미소면적 ds벡터와 180도가 된다. 그러면 r∧ds-> 는 스칼라량이 된다.
따라서, ∫ -(GM/r2)r∧ds-> = ∫ -(GM/r2)ds 가 되어 계산이 간단해진다.
공대 전자기학에서 하는 그림이다. 축구공 껍질을 좌표에 그리면 r, Θ, Φ 가 되고, 계산은 얇은 껍질의 면적을 구하는 것인데, 각 변은 rsinΘdΦ와 rdΘ가 되어 면적 ds=r2sinΘdΦdΘ가 된다. 어쩌면 물리학 하기 전에 직각좌표에서 구좌표로 좌표변환부터 훈련해야 한다.
따라서, ∫ -(GM/r2)ds = -GM∫02πdΦ∫0πsinΘdΘ 가 되는데,
Φ는 경도이므로 0~2π까지 적분해준 ∫02πdΦ=2π가 되고, Θ는 위도이므로 0~π까지 적분해준 ∫0πsinΘdΘ=〔cosΘ〕0π이=-2가 된다. 따라서,
-GM∫02πdΦ∫0πsinΘdΘ = 2πGM〔cosΘ〕0π = -4πGM이 된다.
M은 지구질량이므로 M=∫vρdv
따라서, -4πGM = -4πG∫vρdv
가우스법칙에서 –4πG∫vρdv = ∫v▽.gdv
따라서, ▽.g = -4πGρ
g는 중력이므로, g벡터는 지구의중력장 Φ에서 왔으므로,
g=-▽Φ 로 적을 수 있다. g는 gravity force vector이고, Φ는 gravity field scalar이다.
따라서 g=-▽Φ를 ▽.g = -4πGρ에 넣으면,
▽.(-▽Φ) = -4πGρ
▽2Φ = 4πGσ
Poisson equation 이다.
푸와송방정식이 아인슈타인 중력장방정식의 3차원 버전이다. 아인슈타인이 이미 유도되어 있는 이 방정식을 등대로 하고 나아갔다. ⌈00μ = -(1/C2)▽Φ 와 ▽2Φ = 4πGσ에서 Φ가 같은 것이다. 이 둘을 도킹시켜 K값을 구하고자 하였다.
K값을 구하기 위해, 중력장방정식의 시간 텀 R00를 구한 것과 리체텐서의 R00를 구한 것을 비교하는데, ⌈α00 이 나와서 이 값을 알려고 측지선방정식에 00텀을 넣어보니 가속도 형태로 뉴턴의 운동방정식이 나왔다. 측지선방정식이 뉴턴의 운동방정식의 4차원 버전이라는 것이 증명이 된 것이다. Force에서 ▽Φ를 통해 Field로 왔다.
#3
다음은 어디를 건드려야 하나 하면, g00를 구해야 한다.
Rμν -> ⌈μνα -> gμν 로 미분을 통해 가는 과정이다. R00를 구했고, ⌈00α를 구했고, g00를 구하면 된다. 지금은 구조만 보면 된다. K값을 구하는 것이다. 공부는 한꺼번에 되지 않는다. 3단계를 모두 거쳐야 한다.
Christoffel(⌈)이 무엇인가? 굉장히 어렵다. 곡선좌표계를 따진다. 한 점에서 접선을 그은 것을 접선기저벡터라고 하고, 법선을 그으면 법선기저벡이다. 점을 이동시켰을 때 접선과 법선벡터를 해 보는 것이다. 벡터가 이동하였을 때 두 벡터의 차이가 크리스토펠이다.
⌈ijρ=(1/2)gkρ(gjk,i + gik,j – gij,k) 이다. 암기해야 한다.
우리가 알고싶은 것은
⌈00ρ = -(1/2)gkρg00,k) = -(1/2)▽g00 이때 ,k 는 미분이다.
⌈00μ = -(1/C2)▽Φ 와 비교하기 위해 당겨오면,
-(1/2)▽g00 = -(1/C2)▽Φ
따라서 g00 = -2Φ /C2
Φ는 지구의 중력포텐셜이므로, Φ=-GM/R =1.3×10-9이다. 지구의 질량에 의해 지구 주위의 시공이 휘어진 비율이 13억분의 1이라는 뜻이다.
Roo = -(∂/∂xα)⌈00α 이고, ⌈00α = -(1/C2)▽Φ 이므로,
Roo = -(∂/∂xα)(-1/C2)▽Φ = (1/C2)▽2Φ
또한 R00=(k/2)σC2이 있으므로, 비교하면,
(1/C2)▽2Φ = (k/2)σC2이 된다.
푸와송방정식에서 ▽2Φ = 4πGσ 이므로,
(1/C2)(4πGσ) = (k/2)σC2이 된다.
따라서 구하려는 K=8πG/C4 이 나온다.
고전역학의 뉴턴역학, 만유인력법칙, 푸와송방정식이 들어가서 푸와송방정식을 가이드로 하고, 중력장방정식에 R00 구하고, 리치텐서에서 R00 구하고, 측지선방정식에 크리스토펠의 00를 구하는 과정에서 나온 가속도의 Force와 뉴턴의 중력장 Φ를 물고 늘어졌다. 아인슈타인 방정식이 뉴턴역학을 다 알아야만 알 수 있는 세계이다. 거대한 2개가 만나서 정답을 찾아냈다. 이 과정에서 아인슈타인이 과거에 유도한 것이 4차원 버전이 맞음을 증명해 버렸다.