수업후기

#0
어떻게 아인슈타인이 상대성 이론에 도달했는가? 당시 대가급들이 많았고, 아인슈타인은 신출내기였다. 톰슨이 전자 전하량과 질량비를 구했는데, 워낙 유명한 실험이다. 그 제자 7명이 노벨상을 받았는데, 대가급이 측정 데이터를 내 놓으니 측정데이터를 검정하는 실험에 들어갔다. 전자의 속도가 광속도의 30% 영역 안으로 들어가면 전자질량이 증가하는 것 같은 느낌이 든다는 것이다. 이것이 아인슈타인 발견한 결정적 지식이다. 그것이 어떤 현상인가? 전자질량이 바뀐다는 것이다. 1800년대 후반 사람들에게 이 사실이 어떻게 느껴지겠는가? 뉴턴역학의 F= ma에서 질량은 안 바뀐다. 질량에 가속도를 주면 힘이 생긴다는 것인데, 힘과 가속도는 바뀌지만 질량이 바뀐다는 것은 아무도 상상하지 못했다. 그런데 전자의 전자기적 현상을 연구하다가 전자의 질량이 바뀔 수 있다는 것을 처음으로 알게 되었다. 뉴턴적 기계역학은 당시 100년 동안 전 유럽의 과학자에게 신적인 존재였다. 당연히 질량이 바뀐다는 것은 있을 수 없는 일이다. 그런데 바뀔 수 있다는 근거가 조금씩 쌓이게 된다. 뉴턴의 메커니즘이 통용이 안 되는 어떤 물리시스템이 있을 수 있다는 생각으로 기울어지기 시작했다. 그것이 전자기적 현상이다. 물리학계가 서서히 기존의 골리앗 거인인 뉴턴 메커니즘에서 다른 세계관이 있다는 것을 알게 된 것이 톰슨 실험을 사후검정하기 위한 실험에서 시작되었다. 거시세계는 뉴턴역학이 너무 완벽히 설명했다. 천체역학은 신학과 연결되니, 종교와 모든 것이 뉴턴역학이 단일세계관으로 통일하였는데, 전자기 현상에서 질량이 바뀌는 현상이 발견된 것이다. 과학자 소수는 돌맹이와 전자의 현상을 모순되게 놓아두면 안 되니 통합된 이론으로 결합시켜야 하겠다는 일단의 프론티어가 출현했는데, 거기에 첫 홈런을 친 사람이 아인슈타인이다. 큰 맥락이다. 전자기현상도 100년 동안 해 오면서 애들 장난 비슷하게 시작했다. 일부 학자가 관심가진, 메인이 아니었는데, 몇몇 학자들이 꾸준히 하다가 완전히 흠집이 나기 시작한 것이 뉴턴 메카니즘이 설명하지 못하는 웨이브적인 현상이 있다는 것을 알게 되면서이다. 뉴턴 메커니즘은 웨이브적 현상이 없으니 완전히 세계관이 뒤집어 졌다. 공부를 많이 한다고 결정적 지식을 만나는 것이 아니다. 전체적 상황에 대한 다른 관점, 전체적 상황에 대한 어쩌면 다른 정답이 있을 것 같다는 느낌을 갖고 있어야 한다.

#1
첫 번째 공식 F=ma로 물리학이 시작되었다. 벡터를 표기했는데, 알면 생략하면 된다. 헷갈리지 않을 자신이 있으면 생략하면 가지고 다닐 수 있어 활용도가 높아진다. 모든 공부의 원칙은 단순화할 수 있으면 최대한 단순화시키는 것이다. 이 공식이 지금까지 발견된 가장 위대한 공식이다. 전자공학도 이 공식 하나를 풀어 쓴 것이라는 것을 알게 되면서 뉴턴이 인류역사에 얼마나 영향을 미쳤는지를 느낀다. 아인슈타인도 뉴턴역학을 4차원 버전으로 바꾼 것뿐이다. 과학사에서 단 한사람을 꼽으라면 아인슈타인 보다 뉴턴 쪽에 더 많이 설 수 있다.
두 번째 공식은 F=ke2/r2 이다. 쿨롱의 법칙이다. F=ma를 다른 공식으로 적으면 F=Gm1m2/r2 인데, 쿨롱의 법칙을 다르게 적으면, F=kq1g2/r2이 되어 완전히 대칭이다. 아인슈타인이 끝까지 연구하고 싶었던 것이 중력과 전자기력을 통합하고 싶었는데 못했다. 모든 학자들이 놀란 것은 중력이나 전자기상호작용이 거리의 제곱에 반비례한다는 것이고 인류의 뇌리에 심어졌다. 질량1, 질량2에서 하나는 지구면 하나는 달, 하나는 사과면 하나는 지구, 하나는 태양이면 하나는 지구, 하나는 갤럭시1, 하나는 별이다. 전하량1, 전하량2는 전자 2개 사이에 일어나는 경우는 e2로 적는다.
하나는 중력이고 하나는 전자기상호작용인데 어디에 적용하는가? 중력은 탄도계산에 사용되고 하나는 감전되고 번개 치는 공식인데 어떻게 만날까? 원자에서 만난다. 원자핵이 지구면 전자를 달로 바꾸면 된다. 이 착상을 구체적으로 한 사람이 닐스 보어이다. 원자를 이해하게 된 것이 이 두 공식을 “같다”라고 두면서 원자의 태양계 모델이 나오면서 부터다. 얼마나 결정적 지식인가 하며 이 두 공식을 결합시키면 곧장 원자핵 주위를 도는 전자의 반지름과 에너지 레벨이 나온다.
F=ma와 F=ke2/r2을 같이 놓고 보니, 원자의 태양계 모델에서 전자가 도는 원운동 가속도를 구해야 하는데, 구하기가 쉽지 않다. 지금 하라고 해도 못한다. 물리학 훈련한 사람도 할 때마다 버벅거린다. 원운동의 가속도 구할 필요 없다는 것을 알려준다. 이것이 결정적 지식이다.
속도(V)와 주기(T)를 곱해주면? 주기는 시간이다. 속도와 시간의 곱은 거리이다. 원에서 거리는 원주이다. 그래서 V.T=2πR이다. 물리학 박사도 헷갈릴 수 있는 것이 벡터이다. V와 R은 벡터이다. 구하고 싶은 것은 a라는 백터이다. 가속도(a)의 차원은 분모는 시간의 제곱이고, 분자는 거리이다. 곧 a=dv/dt=V/T이다. V=aT가 되어, aT=2πR/T가 되어, a.T=2πV이다. 아름답다. 가속도에 시간을 곱해주면 속도차원이 나온다. 가속도 a=2πV/T에서 T=2πR/V를 대입하면, a=2πV/(2πR/V)가 되고, 정리하면 V2/R이 된다. 암기 필요없다. 적으면 된다.
F=ma=mv2/r, F=ke2/r2 이므로, mv2/r=ke2/r2이다. 구체적으로 r을 알고 싶다. 전자가 핵에서 얼마나 떨어져 도는가는 정확하게 달이 지구에서 얼마나 떨어져 도는가와 같다. mv2r=ke2이 된다. 구하려는 r=(ke2)/(mv2)이 된다. 전자의 전하량 e, 전자의 질량 m은 알고 있다. 그런데 속도를 모른다. 죽었다 깨어나도 속도를 알 수 없다. 다른 무엇이 필요하다. 닐스 보어가 한 일이다. 양성자가 있고 전자가 돌아가는데 속도를 알고 싶다. 닐스 보어는 이럴 거라고 가정을 했다. 도는 전자의 에너지가 불연속해서 플랑크 상수의 정수배(nħ)에 해당하는 에너지만 갖는다고 주장했다. 증명한 것이 아니다. 여기에 해당하는 고전물리량 반지름(r)×운동량(P)과 같다고 놓았다(r×P=nħ). 닐스 보어가 노벨상 받은 수식이다.
각운동량 L=r×P로 모두 벡터이다. 원운동에서 반지름과 접선은 항상 각도가 90도이기에 L=rp가 된다. 요 값이 양자화 되어 rp=nħ이다. P=mv 이다. 우주론은 포톤에 대해서 4차원 모멘텀 P이다. 우주 전체에서 포톤 알갱이가 날아가면서 모멘텀 P가 어떻게 바뀌었는가를 연구하는 학문이 우주론이다.
따라서 mvr=nħ에서 v=nħ/mr이 된다. 훈련이 되면 초등학생 일기장 쓰는 것과 같이 단순하다. 따라서 r=(ke2)/(mv2)의 v에 대입하면, r=(ke2m)r2/(n2ħ2)이 된다. 따라서 r=(n2ħ2)/(ke2m)이 된다. n은 정수이다. rn=(ħ2/ke2m)n2이다. 전자에 해당하는 상수를 넣으면 r=0.53A(옹그스토론)이 된다. 몇 단계 만에 전자의 반지름을 구했다. 일반화하여 rn=a0n2로 적는다.

2
다음에 에너지를 구하면 E=K.E+V.E이다. 운동에너지(K.E)는 1/2mv2이고, 포텐셜에너지(V.E)는 어려운데, 힘을 적분하면 에너지가 된다. F=ke2/r2을 r에 대해 적분하면 V.E=–ke2/r이 된다. 따라서 E=1/2mv2-(ke2)/r 에서 mv2=ke2/r 이므로, 대입하면 E=-ke2/2r이 되고, r=a0n2을 넣으면 =-ke2/2a0n2이 되고, -ke2/2a0는 모두 상수이고 –E1이 된다. 따라서 –E1/n2으로 적는다. E1은 수소에서 전자 하나를 떼어내는데 드는 이온화 에너지로 E1=-ke2/2a0 = -13.6 eV이다. 1eV=11,600도이므로 이 에너지는 온도로 15만도에 해당하고, 이때 전자는 자유전자가 된다.
왜 –를 붙여주는가? 양성자가 있으면 쿨롱 우물이 아래에 있어서 양성자가 에너지 0이고, 전자가 –13.6eV이다. 그래서 13.6 eV의 에너지를 주면 전자가 0 위치로 올라와서 자유전자가 되는데, 우리가 볼 수 있는 자유전자는 번개이다. 온 몸으로 느끼는 자유전자는 감전이다. 이것이 현대물리학의 핵심이다. 10분 만에 끝난다. 이것밖에 없다. 뉴턴의 만유인력 법칙의 위대함을 보여준다.
수소원자 이외의 원자에 대한 일반화된 공식은 원자번호가 커질수록 반지름은 줄어들고 에너지는 커진다. rn=(a0/z)n2 이 되고, En=-(Z2E1)/n2이다. Z은 원자번호이다. X선 에너지가 가시광선 1000배가 되는 것은 구리 29번에서 나오므로 제곱하면 900이 되기 때문이다.
맥스웰 방정식이든 원자론이든 300년에 걸쳐서 유럽에 서양사람들이 300년 동안 하나하나 각축하며 정립한 것이다. 벤자민 플랭클린이 번개칠 때 연 날리는 시험을 했는데 운좋게 살았는데, 이렇듯 목숨 걸고 밝혀낸 것이다.
공식을 다 적어놓고 이것이 어떻게 오게 되었는가 살펴본다. 쿨롱의 법칙, 뉴턴의 법칙, 닐스보어의 각운동량 정의, 이 3개가 들어가 있다. 그런데 닐스보어는 증명한 것이 아니다. 어떻게 맞다고 증명하나? 닐스보어가 그렇다고 둔 것이다. 4차원 세계에 들어가면 맞다는 것이 증명된다. 전체가 로테이션이다.
4차원 벡터이다. 4차원은 공간차원과 시간차원을 합한 것이다. 공간은 x, 시간은 t로 두고 괄호로 두는 것이다. 가장 위대한 점프는 괄호이다. 입자물리학에서도 양성자와 중성자를 괄호로 묶은 로테이션이 문을 열었다. 시간과 공간을 4차원에서 통합을 하고 싶은 것이다. 물리학에서는 단위가 같아야 묶을 수 있다. 시간을 공간으로 바꾸려면 속도를 곱하면 된다. 깊이 생각하면 틀리다. 속도와 시간에서 속도가 바뀌면 차원이 바뀐다. 그래서 무차원인 상수를 붙여야 하는데, 그것이 빛의 속도(C)이다. 그래서 X=(ct, x)로 통합된 것이고 4원 벡터라고 한다.
4원벡터의 크기는 X절대값을 구한다. IXI=√X.X=√(ct)2-(x)2 으로 적는데, 부호가 –이다. 이를 민코프스키 혁명이라 한다. 이것이 어떻게 나왔나 하면, 진공 속에 빛이 반짝이면 파가 축구공처럼 구면파가 된다. 광원에서 구면파까지 거리는 (ct)2=x2+y2+z2이 된다. 이것을 한쪽으로 넘기면, (ct)2-(x2+y2+z2)=0이 되는 이 방정식이 여기 들어간 것이다.
우리가 존재하는 것은 시간과 공간 축에서 원추 안에 있는 것이다. 원추 안은 광속보다 느린 속도로 가는 것이다. 원추 안은 time-like이고, 원추 밖은 space-like이다. space-like에 있는 것은 나와 인과를 맺지 않는다. 원뿔을 꼭지점 뒤로 그려 놓으면 과거가 된다. 무한한 과거에서부터 오는 모든 광속도 이하의 사건들의 총화가 지금 여기에서 만나서 다시 미래로 가는 것이다. 바깥쪽이 없느냐? 있다. 빛으로 가도 도달 못하는 공간이다. 빅뱅 당시 한 점에서 플랭크 타임 때 인플레이션이 일어나서 우주가 광속보다 더 빨리 팽창하였다. 우주 속에 있는 모든 것은 광속을 넘어설 수 없지만 우주 자체는 해당되지 않는다. 138억년 빛으로 가는 우주보다 1000배는 더 큰 공간이 우주에 있다. 광원을 벗어나 있어 여기서 일어나는 우주적 현상은 우리가 있는 우주에 어떤 영향도 못 미친다. 인과적으로 연결되어 있지 않다.
명상가들이 얘기하는 ‘지금 여기’는 존재하지 않는다. 한 점이다. 이 점은 좌표를 어디에 설정하냐에 따라 다 다르다. 우리가 존재하는 것은 ‘환’으로만 존재한다. 존재는 측정해야 하고, △t=0가 되어야 하고, △t=0를 순간이라고 한다. 순간에만 존재가 존재할 수 있다. 그런데 순간은 우주에 존재하지 않는다. 그래서 존재는 존재하지 않는다.
다음은 4차원 속도에 홰당되는 4원속도(U)는 4원벡터(X)를 고유시간(dτ)으로 미분해준 것으로 U=dx/dτ로 쓴다. 특수상대성 이론에서 t=τ/√(1-(V/c)2=γτ 이다. 여기서 속도(V)만이 변수이다. U=(c(dt/dτ), dx/dτ)가 되고, dt=γdτ이고, dτ는 내가 내 시계를 본 것으로 정지시간이고, dx는 내 바같의 공간거리이다. 이것은 dx/dτ는 곧장 미분이 되지 않는다. 한쪽은 τ, 한쪽은 x의 세계이다. 되도록 바꾸어 놓아야 하는데, x의 세계에 해당되는 t를 넣어서 dx/dτ=(dx/dt)(dt/dx)로 바꾸어준다. dx/dt=속도(v)이고, dt/dτ=γ가 된다. 그러면 U=(cγ, vγ)의 아름다운 수식이 된다. IUI=√(cγ)2-(vγ)2=cγ√1-(v/c)2=cγ.(1/γ)=c가 된다.

#3
3차원 속도벡터에 해당되는 것을 4차원으로 바꾸면 시간이라는 텀이 생긴다. 3차원 운동량을 4차원으로 바꾸면 시간 텀이 생기는데, 이것이 에너지가 된다. 그래서 전체를 4원 운동량 벡터라 부른다. 그래서 물리학에서 궁극의 방정식은 4원 운동량 벡터이다. 우주론에서 볼츠만 방정식이 일반상대성보다 10배 정도 큰 방정식인데, 포톤의 4차원 운똥량을 구하는 것이다. 그것을 구하는 공식이 200가지이다. 4차원에서 운동량은 운동량과 함께 에너지가 들어가서 4차원 운동량 하나로 우주론 전체를 기술할 수 있다; 이것이 4차원 혁명이다.
4차원 운동량은 정지질량 곱하기 4원속도벡터로 P=moU이다. 따라서 P=(moγc, m0γv)이다. m0γ=m0/√(1-(V/c)2 이다. 이것 때문에 상대성 이론의 공간이 줄어들고 시간이 늘어나는 놀라운 현상이 일어난다. 이 전체 m0γ=m0/√(1-(V/c)2=m이라고 한다.
따라서 P=(mc, mv)가 된다. IPI=√(mc)2-(mv)2=γ(mc2/c)2-p2이 된다. 또한 IPI=√P.P=√((m0U).(m0U)=m0√U.U=m0c가 된다. 양쪽을 등식으로 놓으면 (m0c)2=(mc2/c)2-P2=(E/c)2-P2이 된다. 따라서 E2=(cP)2+(m0c2)2이 된다. 이 공식이 얼마나 위대한 공식인가 하면 여기에 4차원 모멘텀과 에너지가 다 들어 있다.
빛(photon)에 대해 정의하면 정지질량 m0=0이고, 에너지 E=PC이다. 이거 하나 얻고자 여기까지 왔다.
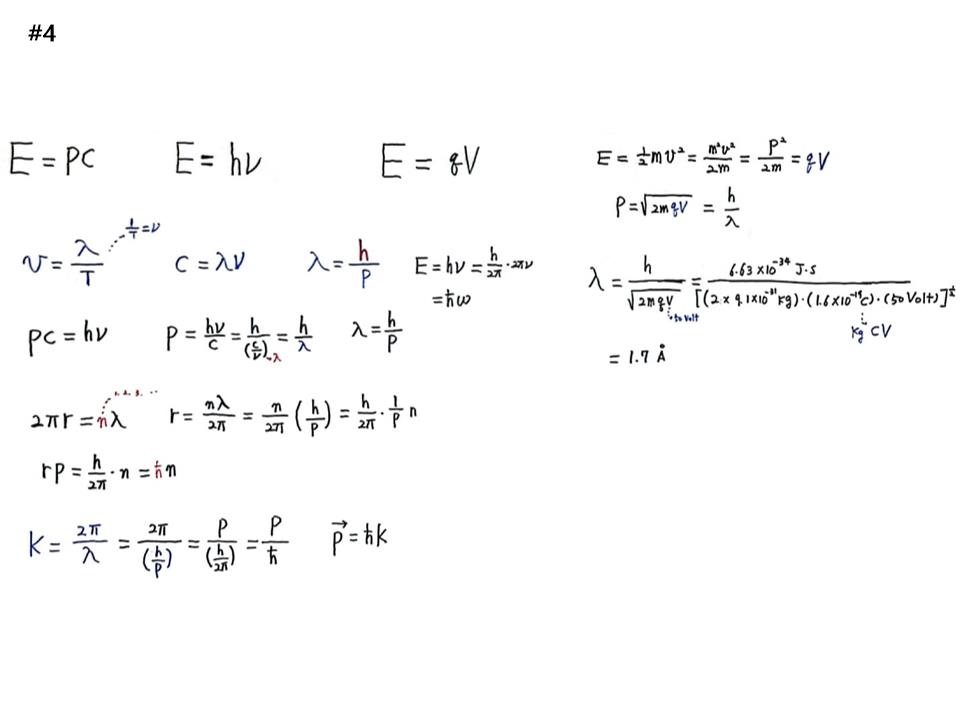
#4
이쪽 공부를 했더니 지금 적는 6개 방정식이 간단한 수식인데, 헷갈린다. 이것만 알면 빛에 대해 다 알 수 있다.
첫 번째 E=PC이다. 빛의 정지질량이 0이기 때문에 드러난 것이다. 두 번째 E=hν이다. 이 공식은 증명하는 것 아니다. 빛의 속성이 양자화된 것이다. 세 번째가 E=qV이다. V는 voltage, q는 전하량이다. 전자의 경우 eV이다. 전자볼트가 곧 에너지이다. Voltage는 전위차이다. 전장과 링크되어 있다. 출처가 다 다르다. 첫 번째 공식은 아인슈타인 1905년도 특수상대성 이론 이후 4차원 개념에서 나온 것이고, 두 번째 공식은 1900년대 초 무렵 양자역학에서 나왔고, 세 번째는 1800년대 전기현상에서 온 공식이다.
다음은 보조공식으로, 파동의 속도를 어떻게 구하는가? 파동의 속도는 한 파장이 지나가는데 시간이 얼마나 걸렸는지가 주기이고 그 역수가 파장이다. 파동의 골짜기와 골짜기 사이거리가 파장 λ로 적고, 걸린 시간이 주기 T이다. 따라서 속도(v)=λ/T이다. 주기의 역수(1/T)는 주파수(ν)이다. 빛의 속도는 C이므로 C=λν이다. 여기서 네 번째 드브로이의 물질파 공식인 λ=h/P이다. 요 공식 하나로 드 브로이는 박사학위 논문이 노벨상을 받았다. 아인슈타인이 이 식을 보고 경악하고, 증명이 되고 곧장 노벨상 받았다.
드 브로이 물질파 공식은 4차원 에너지와 양자역학 에너지를 결합하면 증명이 된다. PC=hν 에서 P=hν/C=h/(C/ν)=h/λ 가 된다. 위치 바꾸면 λ=h/P가 된다. 포톤의 존재는 4차원 존재이고 양자화 되어 있으니 같이 쓸 수 있다. 그러면 바로 물질파 공식이 증명된다. 이 공식이 대단하다. 앞서 –로 적겠다는 민코프스키 혁명에서 우리는 시공이 결합되어 있다는 것을 알게 되고, 거기서 4차원 에너지가 주어지고, 양자에너지와 결합하니 물질파가 나왔다.
다음은 닐스보어는 모든 것이 파동이라고 보면 파동의 개수를 어떻게 헤아리는가? 파동은 영원히 무한대 공간으로 가는데 파동의 개수가 무슨 말인가? 원을 두고 파동을 원에 맞추어 보면 그 마디를 카운트하는 것이다. 주파수를 높이면 갯수가 많아질 것이다. 어떤 파동도 원에 맞추면 된다. 그러나 어떤 파동은 결이 맞지 않으면 곧장 감쇄되어 사라진다. 딱 맞는 파동을 양자수(quantum number)라고 한다. 여기서 주기율표가 만들어져서 존재가 왜 존재하느냐를 얘기한다. 이것이 정형파이다.
원의 둘레는 2πr이다. 그러면 원의 둘레에 맞는 파장이 몇 개 들어가는가? λ에 정수 n을 붙이면 된다. 따라서 2πr=nλ가 된다. r=nλ/2π=n(h/P)/2π=n/2π(h/P)=(h/2π)(1/P)n이 되어 rP=(h/2π)n=ħn이 된다. 따라서 닐스 보어가 “두자”라고 했던, 다섯 번째 공식인 mvr=nħ가 증명이 되었다. 증명을 해 준 드 브로이 물질파 공식은 양자역학과 4차원 에너지 공식에서 왔고, 4차원 공식은 X=(Ct, x)에서 왔다. 여기에 전율해야 한다. 지난 100년동안 현대물리학 흐름이 이 속에 있다.
다음은 반도체에서 많이 쓰는 K벡터이다. K=2π/λ로 정의한다. 양자화 시켜본다. 드 브로이 물질파 공식이 파워풀하다. 아인슈타인이 이 공식 홍보를 다 해준다. 이 공식이 나오고 나서 지금까지는 물질과 파동을 따로 보았는데 서로 왔다갔다한다는 것이다. K=2π/λ=2π/(h/P)=P/(h/2π)=P/ħ 이다. 따라서 여섯 번째 반도체 물리학에서 쓰는 공식으로 P=ħK이다. 덤으로 E=hν를 변형하면 E=hν=(h/2π)2πν=ħω를 사용한다.
이렇게 모아 놓은 데가 없다. 3가지 빛의 에너지의 절대적 공식, 그리고 드 브로이 물질파 공식. 닐스보어 공식, K벡터 공식은 무조건 외워야 한다. E=PC를 몇 번 유도하고 나면 안 헷갈린다. 서로 증명이 된다.
구체적으로 어디에 쓰이는가? E=qV가 얼마나 파워풀한가 예를 들어 보여준다. 전자가 50V로 가속한다면, E=(1/2)mv2=(m2v2)/2m=P2/2m=qV이다. P=√2mqV=h/λ가 되고, λ=h/√2mqV=(6.63×10-34 J.S)/√(2×9.1×10-31 kg)(1.6×10-19 C)(50 V)를 계산한다. 답은 λ=1.7A(옹거스트론)이 나온다. X-레이 파장이 된다. 전자가 50V로 가속되면 X-레이 파장이 됨을 보여준다.
#5
피타고라스 정의 증명법이 수백 개이다. 브레인 친화적 증명법이 있다. 보는 즉시 아는 단순한 증명법을 갖고 가야 한다. 도형도 다 빼야 한다. 아름다움을 훼손한다. 순수하게 기호로써 보면 기억이 된다. 그냥 맘대로 될 수 있는 단계가 되면 의미를 따질 수 있는 인지능력의 여유가 생기고 그때서야 바라보기가 가능해진다. 가장 축약된 로테이션을 가지고 있으면 풀어 쓸 수가 있다.
맥스웰 방정식은 대단하다는 것을 다 내려놓고, 하나도 신비스럽지 않고, 하나도 어려운 것 아니다. 맥스웰이 1861년에 논문을 썼다. 아인슈타인이 아무리 위대해도 1905년이면 100년 전이다. 아무리 대단해도 지금은 중학생도 이해하는 수준이다. 그 당시 과학자가 그리 대단하지 않다. 당시만 홰도 연금술과 과학이 구분이 안 된다. 지금은 인터넷도 쓴다. 모든 공부는 신비를 벗기면 다 중학생 수준이다. 우상화하고 천재가 했다고 생각하는데 지금 보면 아무것도 아니다.
뢴트겐 X선이 과학사를 바꾼 이유는, 우리 사람들은 눈에 보여주면 놀라워한다. 많이 배웠거나 적게 배웠거나 기적을 보여주면 세계관이 확 바뀐다. 기독교가 공인된 것도 콘스탄트 대제가 전쟁에 나가서 십자가를 하늘에 보여주어서 확 바뀌어졌다. 기적같은 것을 보여 준 것이 앙페르이다. 도선에 전류를 보내니 나침반이 움직인다. 이 사건을 처음에는 정상급 학자들이 듣고 웃었다. 도선에 전류가 흐르려면 축전지가 있어야 한다. 1800년도에 볼타르가 나폴레옹 앞에서 축전지를 시연했다. 어느 정도 상용화가 된 것이다. 연속적인 전기는 볼타 전지 이후에 출현했다.
앙페르 법칙이 물리학계에 충격을 주었고, 그 여파로 도선에 전류가 흐르면 자기장에 생긴다를 페러데이는 반대로 해서 자석을 움직여 도선에 전류가 흐르는 것을 보여 주었다. 페러데이 법칙이 나중에 나온다. 이 두 법칙을 맥스웰이 4가지 공식으로 집대성한 것이다. 집대성 하는 과정에서 도선이 끊어졌을 때, 교류가 흐를 때 어떤 사건이 벌어지는가? 축전지가 충전되고 방전될 때는 교류가 된다. 이때 어떤 일이 일어나는가를 밝혔다. 이것을 수식한 것이 변위전류로, 이것이 도선이 없는 자유공간까지 확대되어 나중에 전자기파라는 개념으로 확대되었다.
페러데이는 축전지에서 방전되는 상황에서 어떻게 되는가를 보았다. 금속판 2개가 간격을 두고 있는데 콘덴서라고 한다.
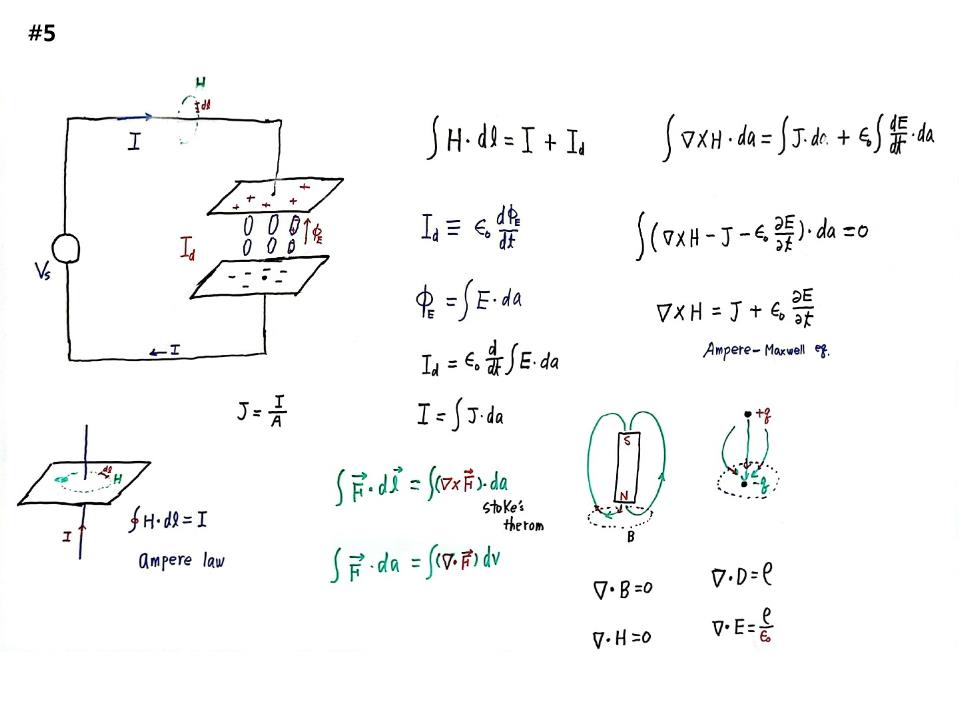
구리 도선에 I라는 직류를 흘려주면 평면에 H라는 자기장이 생겨서 나침반이 움직인다. 공간상에 뭔지 모르지만 힘이 미치는 공간이 된 것이다. H라는 공간의 미소둘레를 dl라고 하고 H를 dl에 대해 적분을 해주면 폐곡선에 있는 전류값 I가 된다. 이것이 앙페르의 법칙이다. 전류와 자석이 첫 번째 링크되는 것을 보여준다.
맥스웰이 한 것은 밧데리에서 충전, 방전할 때 어떤 상황이 벌어지는가를 보여주었다. 전류 I가 흘러서 연결된 금속판에 +전기가 쌓이고, 떨어져 있는 맞은편 금속판에는 –전기가 쌓인다. 그 사이는 절연체를 넣는데, 맥스웰이 가정한 것이 안에 온갖 물질에 국부적 전장이 생겨서 분극이 된다. 변위전류를 정의하여 Id라고 하고, 앙페르 법칙을 적용하여 도선 둘레가 dl이 된다. 페러데이 법칙은 도선 폐회로가 dl 이다.
앙페르 법칙은 도선 둘레에 자기장이 생긴다. 자기장 H를 dl로 적분해주면 Id를 추가하여 I+Id가 된다. 맥스웰은 Id,를 정의하여 Id=ε0(dΦE/dt)가 된다. ΦE는 금속판 사이 절연체에 국부적으로 생긴 전기력선이다. 나중에 페러데이가 자석에서 역선이 생긴 것을 쇳가루를 뿌려서 알게 되었다. 단위 면적당 역선의 개수를 헤아린 것이 패러데이의 길이고, 나중에 아인슈타인 등이 이 길로 간다. 전기에 대해서도 +에서 –로 오는 것을 전기력선 ΦE라고 부르고, 자기력선은 ΦB로 표기한다.
전기력선 다발 ΦE는 전기장(E)을 면적(da)에 대해서 적분해주라는 것이다. Id=ε0(d/dt)∫E.da 이고, 전류밀도(J)는 전류(I)를 면적(A)으로 나누어 준 것이다. 전류(I)는 전류밀도벡터(J)를 면적벡터(da)로 적분해 주면 된다.
임의의 벡터 F를 미소길이(dl)에 대해서 적분해주면 벡터의 컬 값을 미소면적(da)으로 적분해준 값이다. 이것이 스토크 이론(stoke theorem) 이다. 또 하나는 임의벡터 F를 미소면적(da)으로 적분하면 다이버전스(▽)와 F를 미소체적(dv)으로 적분한 값이다. 임의의 벡터에 적용되므로 스토크 공식을 써서 ∫H.dl=I+Id 에 집어 넣는다. 길이적분을 면적적분으로 바꾸어 주는 것이다.
∫▽×H.da=∫J.da+ε0∫(dE/dt).da가 되고, 이항을 하면, ∫(▽×H-J-ε0(∂E/∂t).da=0가 된다. 이 공식이 항상 성립하기 위해 안에 있는 피적분이 0가 되어야 한다. 그러면 ▽×H=J+ε0(∂E/∂t)가 된다. 이 아름다운 공식을 앙페어-맥스웰 공식(Ampere-Maxwell equation)이라고 한다. 앙페르가 했던 주회법칙(Ampère's circuital law)에다가 displacement current(Id)라는 개념을 집어 넣어주어 축전지에 대해 완벽히 설명이 되었다. 이것이 왜 혁명을 일으켰냐면, 자유공간이면 도선이 없는데도 전기가 축적될 수 있다. 그래서 J가 0가 되도, ε0(∂E/∂t)는 0가 아닐 수 있다. 끼워 맞추기 위해 덤으로 집어넣었던 것이 전파공학에 가서는 메인이 되었다.
#6
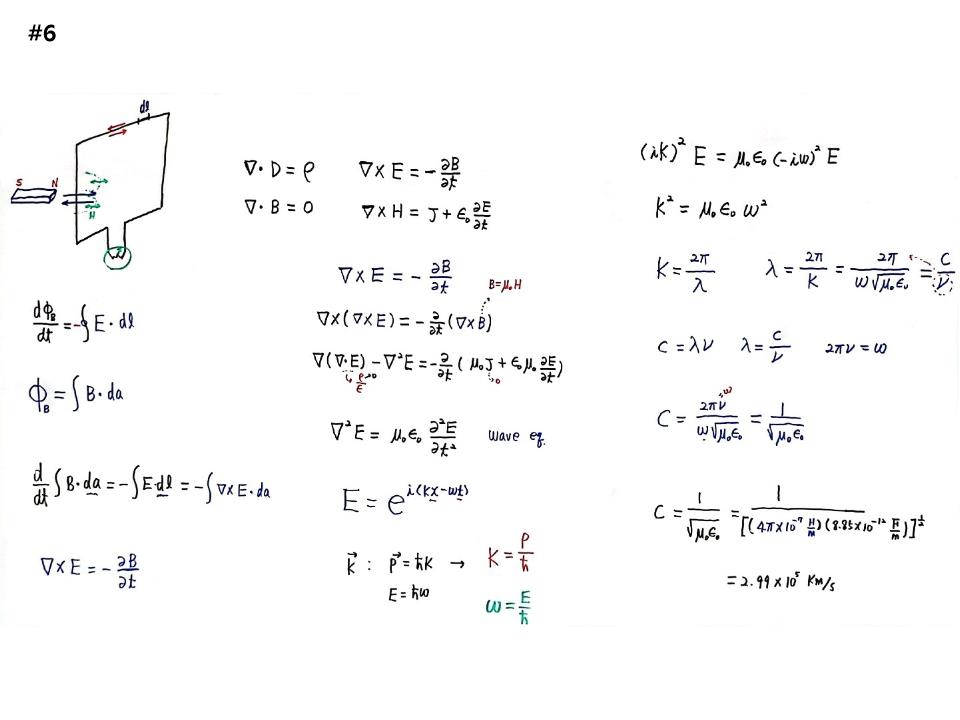
두 번째 패러데이는 반대로 접근했다. 도선을 고정하고 끝에다 전류계 측정장치를 물려 놓은 폐회로이다. 막대자석을 도선에 집어넣었다 뺐다 하니 전류가 이쪽 또는 저쪽으로 흐른다. 이것을 페러데이 전자기유도현상이라고 한다. 자석이 들어가면 자기장이 형성되었다가 이동을 한다. 수식으로 하면 자석밀도(dΦB)가 시간에 따라 함수가 된 것으로 dΦB/dt가 된다. 그래서 생긴 것이 전기인데, 기전력(E)은 선소(dl)에 따라 주회적분을 해주라는 것으로, 수식은 dΦB/dt=-∫E.dl이 된다. 다발의 변이를 일정하게 만들어주기 위해 –를 붙인다. 전속밀도 ΦB는 B벡터를 면적에 대해 적분해 준 것으로 ΦB=∫B.da가 된다. 넣어주면 d/dt∫B.da=-∫E.dl 이 되고, 스토크 법칙을 적용하여 면적분으로 바꾸어 차원을 맞추어 주면, d/dt∫B.da=-∫E.dl=-∫▽×E.da가 된다. 바로 전장의 회전 ▽×E=-∂B/∂t가 된다는 아름다운 법칙이 나온다. 가장 하이라이트이다. B가 뭔가가 핵심이다. B는 테슬라이다. 자기장의 세기가 시간에 따라 바뀐다는 것이다. 그러니 전장 회전을 가지고 온다는 것이다.
다음 현상은 막대자석이 있다면 N에서 S로 자기장이 들어간다. N에서 나오는 자기장을 폐곡선을 만들어 적분을 해본다. 자기장B 둘레를 적분하면 발산이 0가 된다(▽.B=0). 자기장이 B둘레를 들어왔다가 다시 나가기 때문에 적분하면 0가 되는 것이다. 직관적이다. 자석은 N극과 S극이 분리가 안되었기에 적분하면 0가 된다. 전장은 다르다. +q와 –q가 있으면 전기력선이 +q -> -q로 들어오는데, 폐곡면을 그리면 들어오기만 하고 나가지는 않는다. 이것을 공식화한 것이 가우스 법칙이다. ▽.D=ρ 전하밀도가 된다. 자기장 H를 쓰면 ▽.H=0인데, 전장으로 쓰면 ▽.E=ρ/ε0이다.
이상 방정식 4개가 나왔는데, 맥스웰방정식이라고 한다. 정리하면,
▽.D=ρ
▽.B=0
▽×E=-∂B/∂t
▽×H=J+ε0(∂E/∂t)
인류 역사상 가장 위대한 방정식으로 뉴턴방정식과 맞선꼴이다. 전자기 현상과 빛과 어떻게 연결되는가는 맥스웰 방정식을 풀어야 한다. ▽×E=-∂B/∂t의 전체의 회전(Curl)을 구하면, ▽×(▽×E)=-∂/∂t(▽×B)이다. 이것을 풀면 ▽(▽.E)-▽2E=-∂/∂t(μ0J+ε0μ0∂E/∂t)가 되고, ▽2E=μ0ε0(∂2E/∂t2)의 아름다운 공식이 나온다. 이 방정식 이름이 Wave equation이다. 일반적 파동방정식이다. 모든 파동방정식에 맞아 떨어지는 일반화된 답이 있다. 맥스웰방정식도 파동방정식이다. E=ei(kx-ωt)는 자연과학에서 가장 위대한 수식이다. 이 답을 파동방정식 ▽2E=μ0ε0(∂2E/∂t2)에 집어 넣으면, (ik)2E=μ0ε0(-iω)2E가 되고, 정리해주고 다 빼 버리면 K2=μ0εoω2이 된다. 생략할 수 있는 것 다 생략하면 에센스가 보인다. 디자인 법칙은 메시지 아닌 것 제거하면 메시지가 드러난다. 미학의 법칙도 그러하다. K는 반도체공학에서 가장 많이 쓰는 수식에서 나온 것이다.
P=ħK에서 K=P/ħ가 되고, E=ħω에서 ω=E/ħ가 되는데, 전자기학 방정식 E=ei(kx-ωt)을 양자화하면 바로 슈뢰딩거방정식이 나온다. 결론은 파동방정식, 슈뢰딩거 방정식 다 잊어버리고 이 함수 E=ei(kx-ωt) 만 가지고 간다.
K2=μ0εoω2에서. K=2π/λ, λ=2π/K=2π/(ω√μ0ε0)=c/ν가 된다. C=λν, λ=C/ν, 2πν=ω 이므,로, C=2πν/(ω√μ0ε0)=1/√μ0ε0가 된다. 다 풀어보니 광속 C가 나온다. 맥스웰이 여기까지 도달했다. μ0=4π×10-7 H/m, ε0=8.85×10-12 F/m를 넣어주면 C=2.99×10에5승 km/s가 나온다. 이것이 광속이다. 인류역사가 바뀌었다. 가장 축약해 증명해 보인 것이다. 이것이 전자기파이다.
#7
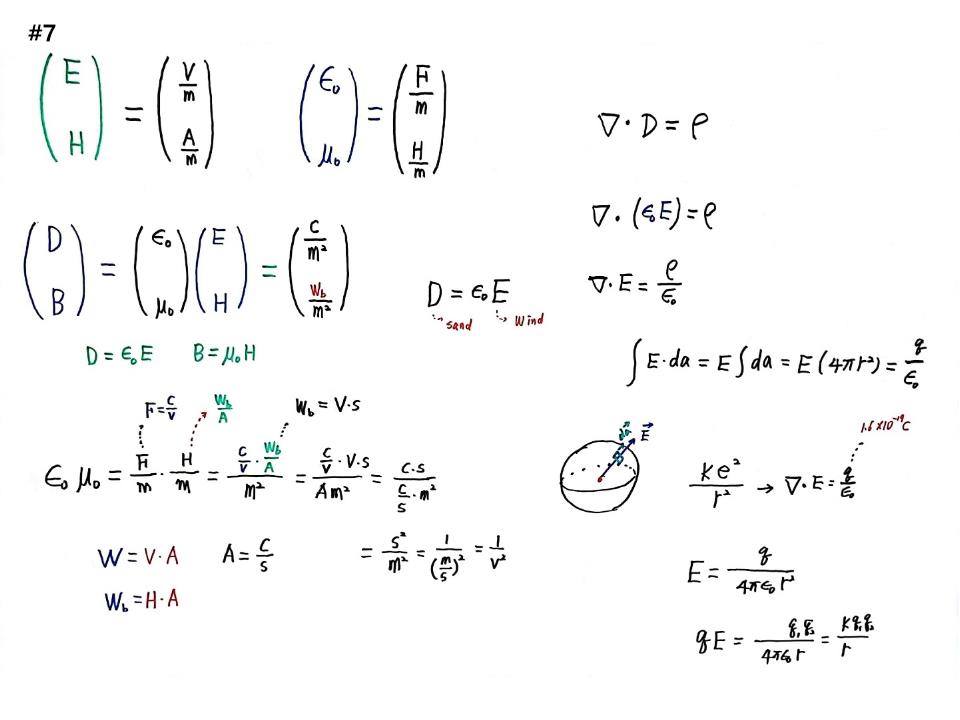
이쪽을 공부하면 단위에 헷갈린다. 전장의 세기 E는 V/m 자장의 세기 H는 A/m이다. 진공의 유전율 ε0는 F/m, 진공의 투자율 μ0는 H/m이다. 전속밀도 D는 ε0E,로 C/m2, 자속밀도 B는 μ0H로 Wb/m2이다. 단위에서 V=voltage, A=ampere, F=Faraday, H=Henry, C=coulomb, Wb=weber, m=meter이다.
μ0ε0가 속도단위가 나오는지 따져본다. ε0는 F/m, μ0는 H/m이므로 두 개를 곱해주면 (F/m).(H/m)이고, F=C/V이고 W(watt)=V.A, Wb(weber)=H.A, Wb=V.s, A=C/s이다. 따라서 (C/V)(V.s)/Am2=C.s/(c/s)m2=s2/m2=1/(m/s)2=1/v2이 되어 속도(v)단위가 나온다.
뉴턴의 세계가 압도적이다. 프린키피아의 충격이 유럽사에 컸는데, 뉴턴역학이 프랑스로 간 일등공신이 볼테르이다. 볼테르가 정치적 압박으로 영국에 도망가서 뉴턴역학의 세례를 받고 프랑스 지성계에 뉴턴혁명을 이야기 했고, 볼테르 연인이 프린키피아를 프랑스어로 번역을 했다. 라플라스가 뉴턴역학을 적용하여 천체역학의 세계적 유명한 책을 쓰고, 이때 나폴레옹이 사관학교 다닐 때 포병학교 교장이 라플라스였다. 나폴레옹이 황제가 되고 라플라스를 지원하여 라플라스 프로그램이 진행되었고 1815년에 나폴레옹이 실각하던 해 끝이 난다. 대략 10년 동안 프랑스 최고 지성인들의 학교에 라플라스 중심으로 푸리에, 푸와송, 온갖 기라성 같은 수학자, 물리학자가 모여서 전부 뉴턴역학을 가지고 거시세계에 대한 천체역학부터 돌멩이 날아오는 것 까지 다 계산하고 물리학은 끝났다고 했는데, 나폴레옹이 실각하고 나서 천천히 터닝을 한다.
뉴턴역학의 치명적 결함이 즉시성이다. 지구와 달이 있고 만유인력이 작동하는데, 시간이 없다. 힘이 즉시 작동한다는 것이다. 이것이 뉴턴역학의 아킬레스건이다. 작용이 미치는데 시간이 걸리는데 뉴턴역학은 시간이 0이다. 대포와 당구공은 즉시적으로 보이는데, 파동은 시간성이 들어간다. 원거리 작용이라고 하는 즉시에 일어나는 말도 안 되는 것이 1815년부터 천천히 금이 가기 시작했는데, 금이 가게 했던 메커니즘이 전자기학이다; 그 전에는 맥스웰 등은 기라성 같은 뉴턴공화국 학자들에게 명함조차 못 내밀었다. 뉴턴은 파동의 입자성이다. 그래서 파동성을 이야기 못 했는데, 나폴레옹이 실각하고 뉴턴 메커니즘이 힘을 잃을 때 새로운 파동이라는 개념이 들어오기 시작했고, 결정적 메커니즘이 전자기학 맥스웰 방정식이다. F=ma의 핵심이 질량이 고정되어 있다는 것이고, 두 개의 질량 사이에 힘의 작용이 아무리 멀리 떨어져도 즉시적이라는 것이 말이 되는가? 안드로메다 200만 광년 떨어진 곳에서 중력이 곧장 작용하는가? 우리는 지금 알고 있다. 지금 태양이 갑자기 사라지면 언제 사라진 것을 알게 될까? 8분 20초 후에 알게 된다. 뉴턴역학에서는 즉각 없어져야 한다. 뉴턴역학은 시간이 안 든다.
나폴레옹이 실각하고 라플라스 프로젝트가 스톱하고 전자기학 시대가 온다. 전자기학 시대에 맥스웰 방정식이 헤르츠 실험으로 증명이 되고, 그때가 되면 해저케이블 까는 전기시대가 온다. 아인슈타인 가정이 전기공구상이었다. 전기가 일반화되고, 특수상대성 논문 제목이 <전자기장 속에서 이동하는 물체의 운동에 관해서>이다. 전자기장 속에서 도체에 관한 것이다. 자석을 이동하면 전기가 생기는데, 자석을 고정하고 도선을 이동해도 전기가 생기는데, 자기장의 변화는 일어나지 않는 비대칭에 아인슈타인은 불편해 하였다. 자석을 고정시키고 도선을 이동했을 때 시공이 어떻게 바뀌는가를 수식화한 것이 특수상대성 공식이다. 정확하게 자기장 속의 도선의 이동이다. 맥스웰의 연장선이 아인슈타인이다. 아인슈타인에서 중력으로 가고 다음으로 우주 전체로 간다. 우주전체로 가는 초석이 맥스웰방정식이다. 힉스메커니즘으로 가는데도 슈뢰딩거방정식이 필요한 것이 아니고 맥스웰방정식 4개이다. 물리학자들이 입자물리학 까지 올라가는데 맥스웰방정식을 제2차 양자화하여 우주론까지 올라간다. 양밀즈이론과 게이지이론에서 맥스웰방정식이 게이지이론으로 바뀌어진다.
웨버가 독일의 최고 학자이다. 가우스와 친하고 가우스가 웨버에게 보낸 편지에서 빛도 원격작용이 아니고 시간이 걸릴거라고 예측을 한다. 빛의 속도를 재려고 최초로 시도한 사람이 가우스이다. 빛의 속도가 무한이면 즉시성이 된다. 그런데 어떤 값을 갖는다면 상황이 달라진다.
맥스웰방정식 ▽.D=ρ에서 ▽.(ε0E)=ρ, ▽.E=ρ/ε0가 되고, 가우스법칙 ∫E.da=E∫da=E(4πr2)=q/ε0 가 된다. 쿨롱법칙 Ke2/r2이 가우스 법칙에서 나온다. E=q/4πε0r2에서 qE=q1q2/4πε0r=Kq1q2/r 이 된다.
E외 D의 관계는 D=ε0E 이다. E는 바람의 세기, D는 모래알갱이이다. 모래알갱이 하나가 전하(charge)이다. ▽.E=q/ε0라는 것은 전하량(q)이 무지 작은량이다. 이것을 ε0로 나누어주면 정확하게 모래알 하나가 나오는 것이다. 맥스웰 당시만 해도 전자기장을 국수다발로 보았다. 조선소에서 샌드블라스팅 할 때 바람이 전기장이고 모래알갱이 하나하나 날아가는 것이 전하이다. 아직 뉴턴역학 그림자이다. 가정이 헤르츠 실험에서 실체로 바뀌면서 과학사가 터닝을 한다.
우주공간에 뉴턴역학은 원거리작용이다. 지구에서 태양까지는 아무리 빨라도 결과는 8분 20초후에 안다. 그 사이에 사라져도 우리는 모른다. 우주공간에는 즉시성이 사라진다. 순간은 사라진다. 뉴턴역학을 많이 하다보면 실체론에 빠진다. 물체가 있어 순간적으로 작용하는 것처럼 속도가 느릴 때는 그렇게 보인다. 이 혁명은 어떠한 힘도 전달되는데 광속을 넘어설 수 없다는 것을 선언한 것이다. 그러면 우주에는 시간은 있어도 순간은 없다. 순간에만 실체가 등장한다. 순간은 없기에 존재는 없다. 존재는 한다. 존재는 측정을 해야 드러난다. 측정은 순간적으로 되는 것이다. 측정은 곧 순간이다. 그런데 이 역학은 순간이 없다.
뉴턴역학이 위대한 역학이다 보니 우리는 착각 속에 산다. 존재한다는 것은 측정하는 것이고 측정은 즉시 보여진다는 것이다. 그런데 즉시는 전자기역학에는 존재하지 않는다. 누가 맞는가? 존재는 측정 즉, 보거나 듣거나 만져야 한다. 뉴턴역학은 보거나 듣거나 만지는데 시간이 안 든다는 것이다. 즉시고 순간이다. 순간을 통해서 존재가 드러난다. 그런데 이쪽 통합된 이론에서는 순간은 존재하지 읺는다. 우리 모든 존재는 환이다. 이것을 밝혀낸 인류 지성사의 혁명이 일어난 것이다. 파동은 속도와 시간이 들어간다. 힘이 미치는데 광속을 넘어설 수 없다. 시간이 출현하였다. 우주에는 시간이 있지만 순간은 없다. 그래서 순간을 통해 출현한 존재는 근거가 없다. 순간을 통해서 존재가 출현한다. 그런데 순간이 없어 존재는 없다. 카를로 로벨리(Carlo Rovelli) 등이 하는 이야기이다.
존재는 그림자인데, 관계의 그림자이다. 사물이 없는데 어떻게 관계가 있는가? 뉴턴역학에 뺘져있어 그렇다. 관계가 먼저 있었다. 누가나 다 관계가 있는데, 관계맺은 사물존재가 모두 사건으로 되어 있다. 내 몸을 점으로 찍어 세포로 나열해 보면 어떤 것은 6시간, 어떤 것은 1년, 어떤 것은 2달, 어떤 것은 100일을 산다. 빠르게 온오프하거나 느리게 온오프하는 과정이다. 우리가 실체로 생각한 것은 모두 과정이다. 우리는 고정된 실체론에 빠져 있었다. 여기에 매스를 가한 것이 톰슨의 실험에서 질량이 바뀐다는 것을 알게 되면서 부터이다. 질량이 곧 실체이다. 세계관이 바뀌게 된다. 아인슈타인이 질량, 시간, 공간이 바뀐다는 것을 보여주었다. 질량이 바뀐다는 것은 뉴턴의 세계관을 벗어나야 한다. 뉴턴의 세계관은 실체론이다. 그런데 질량과 시간과 공간이 속도에 따라 바뀐다는 것이다. 속도는 나의 고유한 속성이 아니다. 속도는 내 것이 아니다. 속도는 공간과 시간의 비이다. 이것을 관계라 한다. 즉 공간과 시간의 관계에 의해서 공간, 시간, 질량이 바뀐다는 것이다. 그간 실체라 생각했던 사람, 지구, 달이 실체가 아니고 시간과 공간의 관계에 의해서 결정되는 것이다. 관계가 먼저고 실체는 변하는 양이다. 상대론적 세계관은 존재에서 이벤트로 바뀐다. 이벤트는 반딧불처럼 점멸하는 것이다. 거기에는 공간도 시간도 없다. 입자는 시간과 공간 속에 사는 것이 아니다. 입자들 속에는 시간과 공간이 대칭이다. 우주에 원래 존재하는 것은 딱 하나 중력이다. 양자화된 중력장에서 시간과 공간이 파생되어 나온다.
지금 우리가 이 공부를 왜 해야 하나? 우리가 질량, 덩어리 중심으로 세계를 보고, 덩어리 사이는 순간적으로 작용했다는 것이다. 순간과 존재가 뉴턴 메커니즘의 핵심이다. 순간이 없다는 것은 모든 작용에 시간이 든다는 말이다. 시간은 존재하는데 순간은 없다. 순간이 사라지니 순간으로 존재했던 모든 사물이 사라진다. 사물이 본질이 아니고 사물대신 들어온 것이 이벤트(사건)이다. 사건의 본질은 관계이다. 관계가 먼저 있고 관계의 그림자로 존재가 따라온다. 왜 물리학을 해야 하는가 이제 이해하여야 한다. 거대한 세계관이 바뀌는 것이다. 우주 전체로 보면 우리가 왜 전자기학을 배워야 하는가? 존재중심의 세계관에서 관계중심의 세계관으로 넘어간다. 곧장 상대성 이론이 나온다. 전자기학은 상대성 이론의 탯줄이다. 뉴턴중심의 세계관이 붕괴되고 들어 선 것이 장세계관이다. 장세계관이 패러데이 역선이다. 패러데이 역선, 필드개념은 처음에 안 받아들여졌다. 그런데 아인슈타인까지 간 것은 필드, 장이라는 개념이다. 필드가 양자화 된 것이 중력장 양자화이다. 장을 양자화한 것이 지금 입자물리학의 최종버전이다.
다시 마무리하면 순간은 존재하지 않는다. 지금까지 순간을 통해 존재가 출현한 원격작용 세계에 살았다. 그런데 우주로 나가면 이것은 착각이라는 것을 알게 된다. 순간은 존재하지 않고 시간은 존재한다. 우주 바깥을 보는 것은 공간을 보는 것이 아니고 시간을 보는 것이다. 안드로메다의 별은 200만년 전에 출발한 포톤이 내 망막에 들어오는 것이다. 모든 것들이 시간을 거슬러 보는 것이다. 전자기학은 인류가 혁명을 일으킨 사건이다.

우.. 와....