수업후기
#0
대한민국이 노벨상이 과학 쪽에 하나도 안 나왔다. 일본은 20개가 넘는다. 노벨상은 1900년부터 시작했는데 지구에서 대단한 상이다. 반드시 증명한 것에 대해서 준다. 노벨상을 받았다 하면 증명되었기에 더이상 왈가불가할 필요가 없다. 증명하는 시간이 걸리므로 20-30년 후에 받는다. 그런데 2-3년 후에 노벨상 받았다면 대단한 것이다. 지난 시간 했던 것에 노벨상이 몇 개인가 세어본다.
디랙방정식 (γμPμ-mc)Ψ=0 은 1928년에 디랙이 유도해서 발표하고 1933년에 디랙이 노벨상을 받았다. 여기서부터 입자물리학이 시작되었다. 디랙방정식은 E2=(PC)2+(mC2)2에서 나왔다. 입자물리학의 공식은 뭐냐고 물으면 이 공식을 적으면 된다. 디랙방정식 유도하는 과정에서 P=-iħ∇를 집어넣고, E=iħ(∂/∂t)를 집어 넣는다. a2+b2=c2 은 제곱의 형태라 아름답지 않다. 그래서 디랙이 했던 것은 a+b=c의 선형으로 표시하고 싶었다. 제곱을 제거하는 과정에서 E=( )+( )로 만드는 것이 수학적으로 어려운 문제다. 디랙이 꿰맞추다 보니 행렬이 들어와야 한다는 것을 알게 되었다. 그 행렬이 γ matrix이다. 인류에게 새로운 시선을 제공했다.
디랙방정식을 증명하는 과정에서 양전자를 발견하고 1936년 엔더슨이 노벨상을 받았다. γ0 행렬의 1열은 전자의 스핀-업이고, 2열은 전자의 스핀-다운이고, 3열은 양전자의 스핀-업이고, 4열은 양전자의 스핀-다운이다. 다시쓰면 행렬이 4개 (Ψ Ψ Ψ Ψ)가 들어있다. 이것을 스피너(spinor)라고 한다. Ψ는 전자의 파동함수인데, 하나로 설명이 안 된다는 것이다. 슈뢰딩거방정식 HΨ=EΨ 에서는 Ψ 하나로 설명이 되는데, 공간에 대해서는 2차 미분(d2/dx2)이고, 시간에 대해서는 1차 미분(d/dt)이다. 그래서 비상대론적 방정식이다. 이것을 시간에 대해서도 1차, 공간에 대해서도 1차로 바꾸어 놓은 것이 디랙방정식이다. 그랬더니 4차원 시공을 다 표현할 수가 있다.
슈뢰딩거방정식은 4차원 방정식이 아닌 고전물리학에 가까운 방정식이다. 어떤 방정식에서 고전물리학과 양자역학을 가르는 기준은 방정식에 플랑크 상수가 들어있는가를 보면 된다. 양자역학이 곧 4차원 시공을 다 담은 것이 아니다. 슈뢰딩거방정식은 시간과 공간이 비대칭으로 들어가 있고 4차원 시공이 아니다. 어떤 방정식이 인덱스에 μ, ν가 나오면 4차원 시공을 담은 방정식이다. 간단하다. 디랙방정식에 γμ가 있어 4차원 방정식의 상대론적 세계이다. 4차원 시공은 하나도 신기한 것이 아니다. 0, 1, 2, 3 로테이션일 뿐이다. 가장 위대한 것은 그 로테이션을 만들었다는 것이다. 세종대왕이 위대한 것은 한글을 만들었기 때문이다. 위대한 학자들을 천재라고 부르지 마라. 그 사람들이 했던 것은 새로운 문자를 만든 것이다. 우리가 모르는 것은 새로운 문자에 익숙하지 않은 것이다. 어렵고 쉬운 문제가 아니고 익숙하냐 익숙하지 않느냐 혹은 내가 색다른 시도를 해봤느냐 안 해봤느냐와 관계있다. 디랙이 위대한 것은 새로운 시도로 γμ 매트릭스를 도입한 것이다.
파울리가 1945년 노벨상 받은 메인 이론이 ’파울리 매트릭스‘이고, 전자뉴트리노를 예측해서 이름을 지어서 노벨상을 받았다. Charm quark로 1976년 노벨상을 받았다. 뮤온뉴트리노도 레더만이 1988년 노벨상을 받았다. 1995년 타우, 2008년 탑쿼크도 노벨상을 받았다. k 메손은 1980년 노벨상을 받았다. π 메손도 1950년 노벨상 받았다. Parity 비보존에서 1957년 노벨상이 나왔다. Ω입자로 머리 겔만이 1969년 노벨상을 받았다. 힉스입자로 2013년 노벨상을 받았다. 표준모형으로 와인버그가 1979년 노벨상, W, Z발견으로 루비아가 1984년 노벨상을 받았다. 겔만 니시지마 식 Q=I3+Y/2 으로 노밸상을 받았다.
노벨상이 여기 15개가 박혀있다. 그래서 졸면 안 된다. 100년 걸린 일이다. 우리가 하고 있는 것이 어느 다리 긁고 있는가는 알아야 한다. 하나라도 박히면 상황이 달라진다.
4차원 시공을 표현할 때 γ 매트릭스는 반드시 들어가 주어야 한다. 4차원 시공은 시간과 공간이 합쳐진 것이다. 3차원 공간의 물리량과 4차원 시공의 물리량은 완전히 다르다. 3차원 공간에서는 시간을 안 따지니 정지라는 것이 있지만, 4차원 시공에는 시간이 기본적으로 들어가 있기에 멈추어질 수가 없다. 모든 것이 흐름이다. 3차원에서 양자역학에서 따질 때는 확률을 따져준다. 4차원 시공에서는 확률이 정지되지 않고 흘러간다. 4차원 시공에 사무쳐야 전체를 이해하는 순간이 온다. 4차원 시간과 공간이 함께 있는 세계를 보았더니 정지라는 개념이 설정이 안된다. 불교에서 이야기하는 것도 이 속에 들어오면 당연한 이야기이다. 하나도 신기한 것이 아니다. 4차원 시공의 모든 존재는 그 자체가 변화이다. 그 속에 항상 시간이 흘러가므로 변하지 않을 수 없다.
이쪽에 다루는 모든 문제가 시공상에서 강물처럼 흘러가는 것이다. 흘러가는 자체는 확률이다. 확률흐름에 관한 것이다. 확률은 실수이므로 ΨbarΨ로 계산하다. 흘러가려면 γμ 매트릭스가 들어가 주어 ΨbarγμΨ 가 되어야 한다. 그래서 모든 것을 설명한다. 이 속에 왜 모든 것이 들어가 있는가 ΨbarγμΨ를 유심히 보라. γμ매트릭스에서 나오는 반전자는 미래에서 현재로 온다고 해석한다. 이 속에 타임머신이 있다. γμ만 쓰면 4차원에 있는 흐름을 표현할 수 있다. 인류가 우주를 이해하는 것은 4차원 시공이다. (iħγ0 ∂/∂t + iħCγ1 ∂/∂x + iħCγ2 ∂/∂y + iħCγ3 ∂/∂z )Ψ = mc2Ψ 에서 4차원 시공은 우주전체 에너지(mc2)와 등호가 되어 t, x, y, ,z축으로 안배를 하는 것이다.
다음의 L = Ψbar(γμ∂μ - m)Ψ + (g1/2)YΨbar(γμBμ)Ψ + (g2/2)Ψbarγμ(τWμ)Ψ + (g3/2)Ψbarγμ(λGμ)Ψ 공식은 집합론적으로 보면 우리가 찾으려는 모든 것이다. 구체적으로 찾는 방법이 γμ에 대한 계산으로 ’클리퍼드 대수(Clifford algebra)‘라고 한다. 클리퍼드 대수가 ’리 대수‘의 한 형태이다. 아무리 날고 기어도 집합론에서 쓰는 로테이션에서 못 벗어난다. 클리퍼드 대수는 γμ에 대한 연산이다. 클리퍼드 대수 연산을 해 보면 Parity가 나온다. Parity는 너무 어려워 못 다룬다. 양전닝과 리정다오가 ’패리티 비보존‘을 이야기하여 전세계 입자물리학자들이 뒤로 나자빠졌다. 그리고 이 이론이 얼마나 충격을 주었으면 보통 20년 후에 노벨상을 받는데, 2년 후에 받는다. 패러티 이 쪽은 우주에 정물질과 반물질이 있는데, “왜 정물질이 더 많은가? 우주가 왜 이 모양으로 되어 있는가?” 를 근본적으로 아는 것이다. 엄청 어렵고 복잡하다. 그리로 들어가는 것도 γμ이다.
L = Ψbar(γμ∂μ - m)Ψ + (g1/2)YΨbar(γμBμ)Ψ + (g2/2)Ψbarγμ(τWμ)Ψ + (g3/2)Ψbarγμ(λGμ)Ψ 공식이 집합론적으로 가장 크다. 이 공식을 푸는 사람들을 입자물리학자라고 한다. 모든 항이 Ψbar( )Ψ 형태이다. 가운데 들어가는 ( )를 빼내보라.
Ψ는 상태함수이다. 양자역학의 Ψn,l,ml,ms로 적는데, 원자핵 주위를 전자가 돌 때 전자는 4개의 상태를 가지는데, 이를 4개의 양자수라고 한다. 양자수는 상수이다. 전자의 파동함수에는 4가지 양자수가 필요하다. 4가지 양자수 외에는 어떤 것도 필요없고, 이 4가지로 주기율표 모든 원소를 100% 설명한다는 것이다. 그래서 우리는 원자에 대해서 정확하게 알게 되었다. 파동함수 Ψ는 어떤 현상을 나타내는 모든 것을 담고 있는 함수이다. 생물학에서 파동함수와 같은 개념은 ’게놈‘이다. DNA는 게놈의 한 형태이다. 게놈이라는 큰 집합 속에 박테리아 게놈, 바퀴벌레 게놈, 개 게놈, 인간 게놈이 있다. 게놈은 그 생물체가 살아가는데 필요한 모든 정보의 집합이다. 대부분은 DNA가 게놈으로 들어가는데, 바이러스는 DNA나 RNA가 게놈이 될 수 있다. 할아버지와 손자를 헷갈려서 학문을 어렵게 한다. 호로자식, 콩가루 집안이 된다. 학문은 위계로 되어 있다. “할아버지가 누군가?”를 먼저 장악해야 한다. 여기서는 모든 것을 담고 있는 것이 Ψ이다.
Ψ가 여러 번 나오는 이유는 전자가 처한 환경이 다르기 때문이다. 전자가 진공 속에 있을 수도 잇고 물 속에 있을 수도 있다. Ψ는 전자 뿐 아니라 쿼크, 뉴트리노에 대해서도 쓸 수 있다. 전자의 파동함수라면 만일 전자가 원자핵 주위를 도는 것이면 양자수로 표시하면 다 끝난다. 그것이 양자역학이다. 만일 베타붕괴에서 나오는 전자라면, 완전히 달라진다. 배타붕괴에는 w입자가 들어간다.
너무 어려운 것을 이해하려니 스트레스 받아 수학이 싫어지고 수포자가 된다. 이해가 안되면 통째로 암기하면 하루 지나면 다 이해가 된다. 이것을 안 가르쳐주니, 다 포기해 버린다. 포기하는 심정으로 암기하면 된다.
몰라도 패턴을 볼 수 있다. 4개가 동일하다. 그러면 90% 알아버린 것이다. 이렇게 동일한 형태로 4개를 쓴 것은 어마어마한 게 들어있다는 것이다. 첫 번째 항 ( )에는 디랙방정식이 들어와 있다. γμ는 동일하게 다 들어가 있다. 그래서 모두 4차원 시공의 흐름이다. 무엇의 흐름인가? 디락방정식은 전자를 설명하는 방정식이었다. 슈뢰딩거방정식의 상대론적 확장버전이기 때문에 전자에 관한 이야기이다. ∂μ, Bμ, Wμ, Gμ는 모두 미분이고 동일하게 μ가 있으니 4차원시공의 미분이다. ∂μ는 전자에 관한 것으로 운동에너지 냄새가 난다. 전자의 순수한 운동에너지와 위치에너지를 나타낸다. Bμ,는 광자에 관한 것으로 전자와 광자의 상호작용을 나타낸다. Wμ,는 W+, W-의 weak boson의 오퍼레이터이다. 따라서 전자와 weak boson의 상호작용을 나태낸다. τ는 σ matrix로 isospin charge가 되고, λ는 color charge가 된다. λGμ는 강한상호작용으로 quark에 관한 상호작용이다. 그래서 전자, 광자. 약한상호작용, 강한상호작용 모두를 포함하고 있는 라그랑지안이다. 다른 말로 우주 전체이다.
공부 잘하는 사람들은 이 공식을 할아버지 비석에 새긴다. 그러면 학자들이 많이 나올 것이다. 우리는 죽어도 학생이다. 무덤에 가서 공부하시라고 비석에 새겨준다. 이것이 할아버지 돌아간 세계 자체이다. 추사체로 적어서 액자로 걸어두어도 좋다.
파울리매트릭스에서 감마매트릭스가 나오고, 겔만매트릭스가 나온다. 3개의 매트릭스만 알면 된다.
쿼크는 (u c t)와 (d s b)로 묶고, 렙톤은 (e, νe) (μ, νμ) (τ, ντ)로 묶어 주어야 안 헷갈린다. spin, isospin 2가지이다. spin은 현실에 발을 담그었기에 직관적으로 알 수 있는 양이다. 그러나 isospin은 순수한 수학적 이미지이다. 핵 속에 quark을 따질 때는 isospin을 쓴다. spin은 돈다는 개념이 절반 들어가 있다. isospin은 spin의 로테이션은 갖고 오지만 완전히 다른 개념이다.
겔만 팔정도 어마어마하게 중요하다. meson은 q와 qbar의 결합이므로 스핀이 0로 나온다. 보존과 같다. isospin공식은 I=(n-1)/2 이다. k입자는 구성요소가 2개인 이중항, π입자는 3개인 3중항이다. n에 들어가는 값이 2중항이면 2를, 3중항이며 3을 집어넣는다. 이것밖에 없다. isospin이 얼마나 황당한 개념인가? 친구 두 사람을 묶으면 2중항, 세 식구를 묶으면 3중항, 이것이 isospin이다. 중은 겹이라는 말이다. 2중항은 두겹, 3중항은 세겹이다. 말이 된다. 묶인 곳에 다른 사람이 들어가면 튕겨나온다. 인간사회에서 진보, 보수 묶으면 딴지 안 건다. 배를 묶고 사과를 묶으면 딴지 안 건다. 여기서 학문이 시작되었다. 1700년대 린네(Carl von Linné 1707~1778)가 식물을 분류하였다, 모과나무가 장미과 식물이다. 모과나무와 장미꽃을 같이 묶는다고 상상할 수 있는가? 이것이 학문이고 isospin이다.
’묶는다‘는 말이 얼마나 중요한가? 이것이 ’집합론적 사고‘이다. 이것이 없어서 사람들이 10-20년 공부해도 헷갈린다. 원자핵이 있는데, 양성자와 중성자가 있다. 양성자는 전기가 +1, 중성자는 0이다. 핵력에서 이상한 사건은 양성자끼리도 당기고 중성자끼리도 당기는데 그 힘이 똑 같다는 것이다. 그러면 핵력에서는 양성자와 중성자를 구분할 필요가 없다. 구분 안 하면 어떤 상황이 벌어질까? 전자기력이 설명이 안 된다. 전자입장에서는 양성자와 중성자가 다르다. 그러나 핵력 입장에서는 다르지 않기에 구분하면 안 된다. 이 간단한 생각을 처음 한 사람이 하이젠베르크이다. 하이젠베르크는 중성자와 양성자를 (n, p) 함께 묶자 하고 같은 것을 Iso라고 하고 isospin이라고 불렀다. 결국 묶은 괄호가 isospin이다. 그런데 묶은 것이 장난이 아니고 명확하게 의미가 있다. 이것이 분류이다. 모든 학문은 분류에서 시작한다. 분류를 하고 나면 달라지고, 이때 상호작용이 일어난다.
묶는 것은 1~4중항까지 있다. 단중항(singlet), 이중항(doublet), 삼중항(triplet), 사중항(quartet)이다. 몇 중항인가가 isospin의 핵심이고, singlet이 중요하다. color charge는 singlet으로 존재한다. 그래서 고립된 입자는 하얀색이다. Isospin 개념이 입자물리학에서 차지하는 비중은 80%이다. 제대로 이해하면 안 어렵다. isospin만 알면 입자물리학 50%는 아는 것이다. Isospin은 “묶자” 주머니이다. 자연은 1중항 형태로 나타난다. meson octet에서 가운데 들어가는 π입자는 3개가 있다. 2개는 8중항(octet)에 포함되고 1개는 8중항에 들어가지 않고 단중항을 형성한다. 어려운 개념이다. 숙달해야 넘어갈 수 있다.
I3는 Isospin의 3방향 성분 중 하나이다. 시계침이 있다면 시계침의 길이에 해당되는 양자수가 L2이다. L2를 파동함수에 오퍼레이션 하면 L2Y=l(l+1)ħ2Y 가 나온다. l(l+1)ħ2는 고유값이고, Y는 고유함수이다. 시계침의 길이는 l(l+1)이 되는데, z축을 수직에서 보면 시계침의 그림자가 z축에 보이는데, z방향 투영값을 I3라고 한다. 시계침이 연속으로 움직이면 그림자가 여러 가지가 있을 수 있으나 양자세계에서는 길이가 1배, 2배, 3배 되는 곳에 있다. 길이가 연속으로 변하지 않고 정해진 양만 양자화 되어 있다. 이를 ’공간양자화‘라고 한다. 중성자의 isospin은 –1/2, 양성자의 isospin은 +1/2이다.
입자물리학은 80%까지 올해 끝내려고 한다. 상대성이론이 응용분야가 3이라면, 입자물리학은 응용분야가 10쯤 된다. 주기율표를 다시 보게 되고, 화학이나, 생물학도 더 깊게 들어가면 관련이 된다. 그래서 입자물리학에 욕심을 내야 한다. 입자물리학은 양자역학에서 나왔고, 양자역학은 고전물리학의 여러 덩어리가 마지막에 입자물리학으로 바뀐다. 그러나 상대성 이론은 하나의 독보적인 존재이다. 상대성 이론은 우주 거시상태를 설명한다. 그래서 지구상에 사는 사람에게는 관련이 없고 유일하게 관련되는 곳은 GPS 정도이다. 블랙홀에 빠져 들어가기 전에는 상대성 세상 못 본다. 입자물리학은 브레인과학부터 모든 뿌리가 연관되어 있다. 수십 개의 학문이 있다면, 다음 가면 단백질, 이온, 분자가 나오고, 다음 가면 주기율표가 나오고, 다음 가면 입자물리학이다. 그래서 입자물리학만 장악하면 나머지는 풀어내면 된다. 그런데 입자물리학을 모르면 애비없는 자식이 된다. 응용 이외에도 입자물리학을 잘 이해하면 인류가 자연을 어떤 방식으로 이해하게 되었는가 노하우를 알게 된다.
#1
물리학에서 대칭은 뭔가? 4가지로 모은다. S, P, I, G를 기억하라.
첫 번째는 Space-time symmetry이다. 여기에는 3종류가 있다. 하나는 translation(병진운동) symmetry이다. 등속도운동으로 돌멩이 던지고, 로켓이 가고, 자전거가 가고, 바람이 불고, 새가 나는 것이다. translation symmetry에서 생긴 것이 에너지(E)와 운동량(P)이다.
물리학자들은 (P0, Pi)로 적는다. 하나로 적을 때는 Pμ로 적는다. 최대한 간단히 한다. μ=0,1,2,3이다. 그러면 Pμ=(P0, Pi)=(E, P->) 가 된다. 다시 적으면 Pμ=(P0, Pi)=(iħ(∂/∂t), -iħ∇->)가 되고, PμPμ=∂μ∂μ-∇2으로 표시된다. 여기에 m이 붙으면 바로 디랙방정식이다.
로테이션이 위대하다. 에너지와 운동량을 하나로 묶었다. 4차원시공에서는 에너지와 운동량을 하나로 보라는 것이다. 에너지는 시간성분의 운동량이다. P벡터는 Pi로 적기도 하고, i=x,y,z으로 공간벡터이다. E는 시간벡터이다. 그래서 에너지는 시간방향의 운동량이다. 왜 대칭이라고 부르는가? 에너지 상수, 운동량 상수이기 때문이다. 모든 양이 아니다. 상수라는 말은 ∂L/∂q=0일 때 나오는 것이 P는 운동량 상수이다. ∂L/∂t=0일 때 나오는 것이 E는 에너지 상수이다. 시간(t)과 공간(q)에 대해서 변화가 0이므로 시공간 대칭이다.
두 번째는 Permutation symmetry이다. 이것이 ‘치환’이다. 이상적인 두 입자를 교환했을 때 대칭이냐 반대칭이냐를 따져준다. f(x)=x2일 때 x->-x를 넣으면 f(-x)=(-x)2=x2이 된다. x를 파동함수Ψ로 바꾸어 놓으면, 어떤 파동함수에서 x대신 –x를 집어 넣어도 동일했다. Ψ(-x)=Ψ(x)를 만족하는 파동함수 대칭을 입자물리학에서는 보존(Boson)이라고 한다. γ, w+, w-, z0 입자이다. Ψ(-x)=-Ψ(x) 로 나오게 되면 반대칭(anti-symmetry)이고, 이것을 만족하는 입자가 페르미온(fermion)이다. e, u, d, ν 등이다. gluon color charge도 반대칭이다. 반대칭은 남자를 바꾸면 여자가 되는 것이지 늑대가 되는 것은 아니다.
세 번째는 Internal symmetry이다. SUL(2), SUC(3)이다. 가장 많이 쓰이는 것은 isospin이다.
네 번째는 Gauge symmetry이다. Global gauge symmetry와 Local gauge symmetry로 나뉜다. Global gauge symmetry는 eiΘΨ로 eiΘ를 파동함수Ψ에 곱해주는 것이다. Θ가 상수이다. 절대치를 취하면 leiΘΨl=lΨl 가 된다. 지구상 모든 사람을 동시에 360도 돌게하면 바꾸어 진 줄 모른다. gauge는 각도(Θ)를 바꾼다는 것이다. Local gauge symmetry는 eiΘ(x)Ψ로 Θ가 상수가 아니고 위치(x)에 따라 달라지는 Θ(x)라는 것이다. 서울에 있는 사람은 90도 돌고 부산에 있는 사람은 15도 돌고, 제주도 있는 사람은 70도 돌면 바뀐 것을 안다. Local gauge symmetry의 대칭을 따져주는 것이 interaction이다. interaction이 자연과학에 4개이다. 중력(G), 전자기력(E), 약한상호작용(W), 강한상호작용(S)이다. E와 W가 합쳐진 것을 Standard model이라고 한다. E를 실어나르는 입자가 γ이고, W를 실어나르는 입자가 w+, w-, z0이고, S를 실어나르는 입자가 gluon이다.
#2
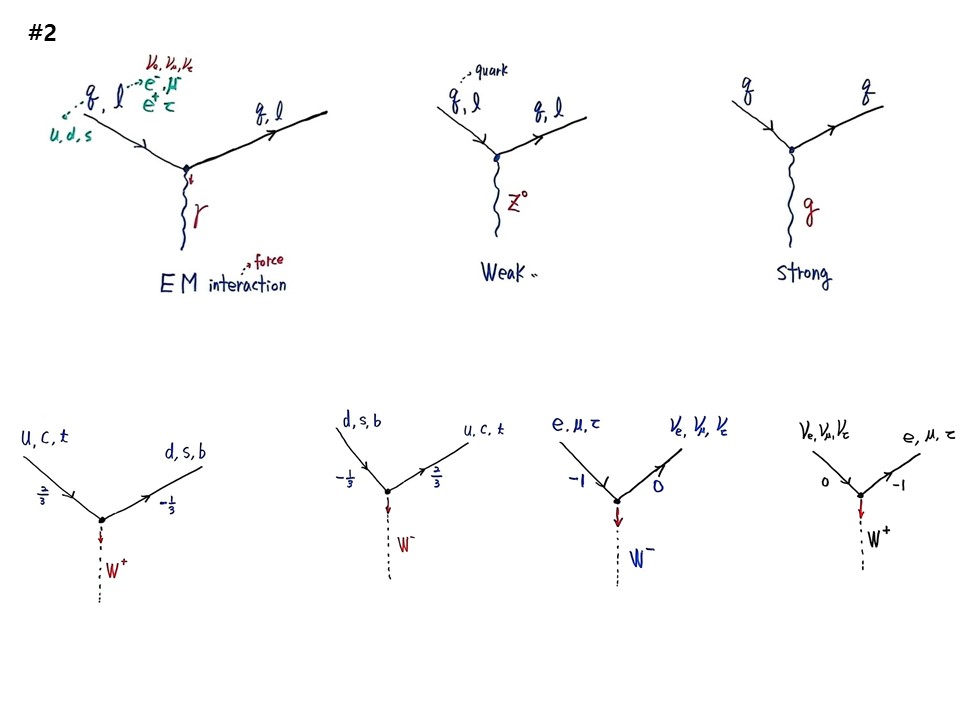
파인만 다이어그램(Feynman diagram)을 그린다. 시공 다이아그램에서 입자가 들어와서 꼭지점(vortex)에서 애를 놓고 몸이 가벼워지니 방향이 달라져서 나간다. 에너지가 빠져나가고 모멘텀이 바뀐다. 첫 번째 빠져나간 것이 γ, 두 번째 빠져나간 것이 z0, 세 번째 빠져나간 것이 g이다. 전부 전기적 charge가 0이다. 첫 번째는 EM interaction 또는 EM force이다. 두 번째는 Weak interaction 또는 Weak force, 세 번째는 Strong interaction 또는 Strong force이다.
첫 번째 quark와 lepton 입자가 들어와서 quark와 lepton 입자로 나가는데, quark은 u, d, s가 오고, lepton에는 e+, e-, μ-, τ가 오는데, 중성미자(ν)는 포톤과 상호작용이 안되어 올 수가 없다. 운동량만 바뀌었다. 에너지도 운동량이다. 운동량은 벡터이므로 화살표로 나타낸다. 에너지는 스칼라로 화살표를 못 쓴다. 두 번째는 quark과 lepton이 오고 quark과 lepton이 나가는데, 운동량 형태의 에너지가 바뀐다. 전기량을 주지 않은 흐름이 생겨서 z0를 중성류(neutral charge)라고 한다. 세 번째는 quark이 오고 quark이 나간다. gluon은 lepton에는 작용하지 않는다. 3가지 힘을 모두 이야기 했다.
다음의 파인만 다이아그램은 첫 번째는 u, c, t가 들어오고, d, s, b가 되어 나갔다. 질량도 다르고 전하량도 다르다. 이때 꼭지점에서 빠져 나간 것이 w입자이다. u, c, t전하량이 2/3, d, s, b의 전하량이 –1/3이므로 w+입자가 빠져 나간다. 두 번째, 반대로 하면, d, s, b –1/3 전하량이 들어오고, u, c, t 2/3 전하량이 나가므로, 꼭지점에서 w-입자가 나간다. 세 번째는 e, μ, τ가 들어오고, νe, νμ, ντ가 나가면 꼭지점에서 나오는 것은 w-이다. 네 번째 반대로 νe, νμ, ντ가 들어오고, e, μ, τ가 나가면 꼭지점에서 나오는 것은 w+이다.
#3
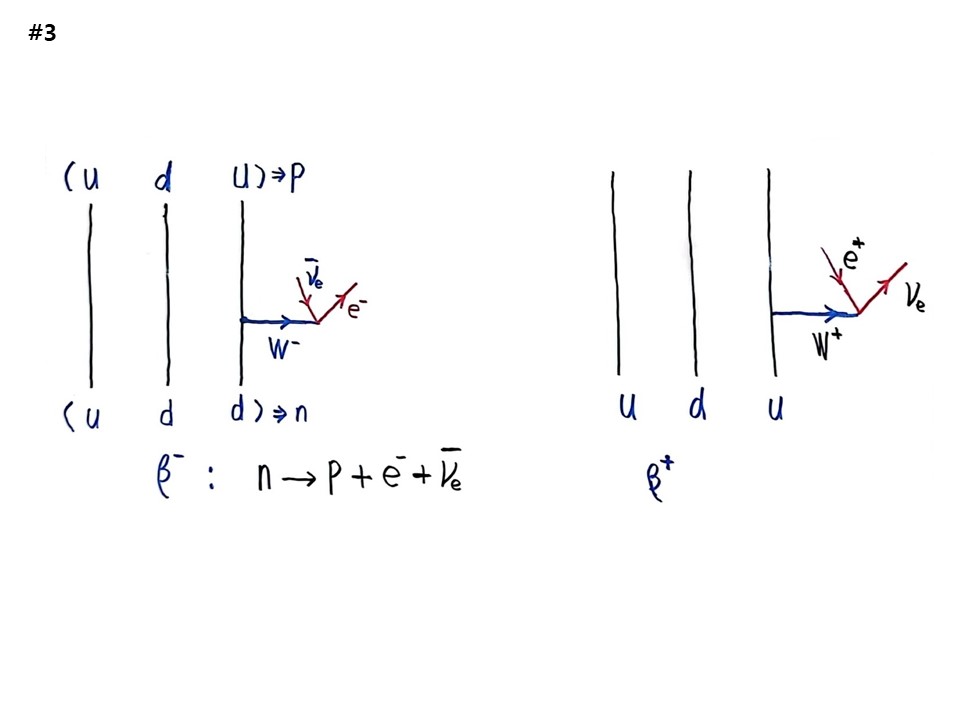
다음 다이아그램은 선이 3개가 나간다. β-붕괴에 대한 것이다. β-입자는 전자이다. 전자가 나오는 붕괴이다. 원자핵에서 튀어나오는 전자이다. 그런데 그 전자는 원래 원자핵 속에 있지 않았다. 전자가 나오려면 출발 입자가 중성자로 (udd)로 표시된다. d에서 w- 입자가 나와서 u로 바뀌면서 한 시공 포인트에서 반중성미자 νebar 입자가 거꾸로 미래에서 현재로 들어가고 e- 입자가 나온다. 그래서 (udu)가 되어 양성자가 된다. 그래서 β-붕괴는 n->P+e-+νebar 로 표시한다. 베타붕괴가 주기율표 전부 다이다.
우리가 아는 전자는 핵 주변을 도는 전자로 물질을 구성한다. 이 전자는 영원히 있다. 처음에는 전자가 원자핵 속에 박혀있는 줄 알았다. 당시 베타붕괴를 알았기에 전자가 원자핵에서 따발총처럼 나왔기 때문이다. 어떤 식으로 전자가 원자핵 속에 있는가를 알아낸 과정이 50년 걸렸다. 원래 있었던 것이 아니고 w입자가 뱉어낸 것이다. d가 u로 바뀔 때 w입자가 나와서 전자와 뉴트리노로 붕괴된 것이다. “원자핵 속에 전자가 있는가?”는 어마어마한 질문이다. 모두 w입자가 하는 일인데 그것을 weak force라고 한다.
전자는 크게 두 가지가 있다. 원자핵 주위에 원래 있는 전자가 있고, 원자핵 속에서 언제든지 상황이 되면 어마어마하게 전자를 내 뿜을 수 있다. 그것이 방사선이다. 방사선은 따발총으로 쏘아대어 아무 데나 박히는 것이다. 단백질 DNA에 박히면 죽게 되는 것이다.
중성자는 나갈 수 있는가? 나갈 수는 있는데 수명이 10분이다. 그래서 어떤 현상이 10분 내로 일어나면 중성자 다발을 볼 수 있다. 우주에서 자유중성자 흐름이 어마어마한 데가 두 군데 있다. 원자력발전소와 슈퍼노바 터졌을 때이다. 원소가 새로 만들어지는 과정이 다 슈퍼노바에서 일어난다. 별 속에서 원소가 만들어지는 것은 1022개의 어마어마한 중성자 다발이 나와서 다른 핵 속으로 들어가면 핵력으로 결합한다.
궁극적으로 모르는 것은 가가 간 줄 모른다. 모든 모르는 근본이유는 어려운 것에는 뭐가 있다고 생각하는 것이다. 모든 것은 묶는 것밖에 없다. 좋아하는 두 사람 묶어서 결혼해서 애 놓아서 박테리아에서 인간까지 된 것이다. 신비한 것이 있어서가 아니고 두 사람 좋아하니 다른 사람과 달라서 묶은 것이다. “묶는다” 외에 아무 것도 없다. 공짜로 묶은 것이 아니다. 서로 좋아하니 묶어 준 것이다. 도깨비와 사람을 묶지는 않는다. 거북이와 사람을 안 묶는다. 사과와 복숭아는 묶지만 사과와 자동차를 묶지는 않는다. 이를 집합론적 사고라고 한다.
최진석 교수가 말하길, “바나나와 침팬지와 사람이 있다면 여러분은 어떻게 묶는가? 동양사람은 바나나와 침팬지를 묶는다. 드러난 작용현상으로 묶는다. 서양사람은 침팬지와 사람을 묶는다. 어느 것이 학문적인가? 사람과 침팬지를 묶어야 한다. DNA가 97% 같다. 여기서 갈라졌다.”
좋아하는 남녀 묶고, 신랑각시 묶고, 야구공과 축구공을 묶는다. 그런데 야구공과 쇠구슬을 묶으면 안된다. 학문은 이것 이상 없다는 것을 깨달아야 한다. 누구도 딴지 못 걸게 묶어야 한다. 입자가 2-3백개 발견이 되었다. 유일하게 할 수 있는 일은 끼리끼리 묶는 것이다. 그런데 눈에 안 보이는 것을 어떻게 묶는가? 누구도 딴지 안 걸게 묶어야 한다. 공동의 성질을 가지고 묶는데, 공동의 성질로 예측을 할 수 있다. “어느 가족의 묶음이 있는데, 다른 가족이 와서 묶을 수 있느냐?”는 간단한 문제가 아니다. 한 가족의 히스토리를 다 알아야 한다. 그 전에는 다른 사람이 가족 속에 들어와도 같은 사람이기에 모른다. 입자물리학에서 묶는 근거가 뭐냐? 근거가 있다. 내부대칭(internal symmetry)이다. 그래서 묶은 것이 SU(3), SU(2)이다. 전기량으로 묶든지, 스핀으로 묶든지, 전부 묶은 것이다. 모든 학문은 분류학이고 언어학이다.
중성자가 양성자로 바뀐 것이 아니고 안으로 들어가 보면 w라는 입자가 나와서 약한상호작용의 결과로 d가 u로 바뀐 것이다. w+, w-, z0 입자는 뚱보로 하나로 묶어서 약한상호작용의 carrier이다. γ는 질량 0로 전자기상호작용이다. 그런데 w+, w-, z0 뚱보와 γ를 함께 묶을 수 있다는 것이 standard model이다. 지금은 아니지만 초기우주 빅뱅 후 100만분의 1초 이전으로 돌아가면 뚱보들이 질량이 0가 된다. 그러면 질량 0로 같이 묶을 수 있다.
주기율표의 할아버지가 베타붕괴이다. 역베타붕괴(β+)를 그려본다. 선3개 그리고, udu 양성자에서 u에서 w+입자가 나오고 e+가 시간역전으로 오면 νe가 시간순행으로 나간다. 그러면 u가 d가 되어 udd 중성자가 된다.
#4
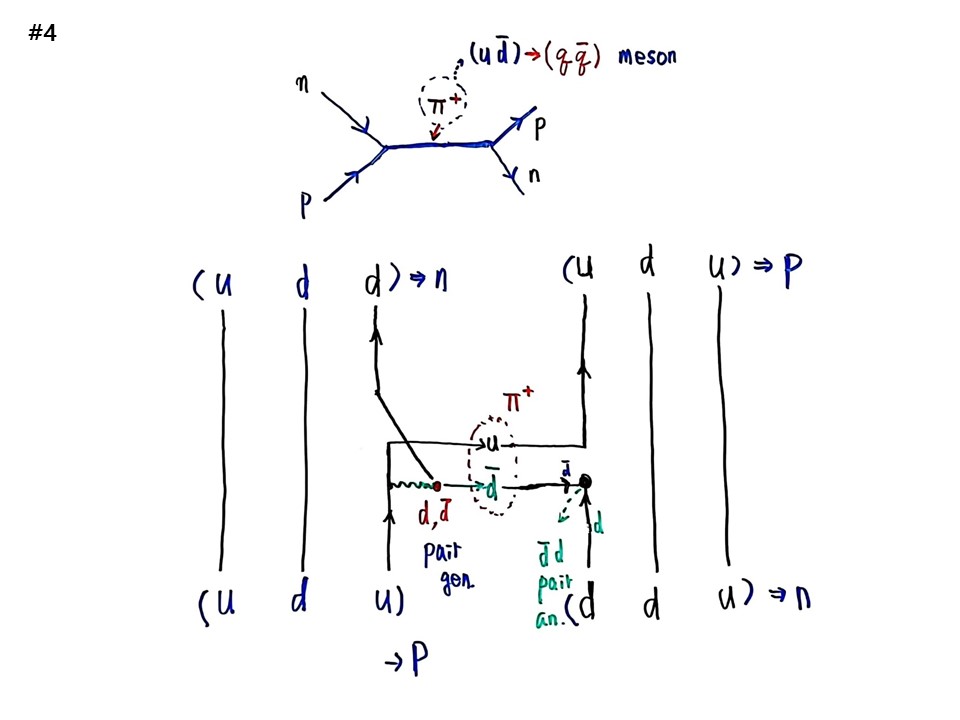
다음은 노벨상 받은 π입자이다. 예전에는 p n 두 입자가 충돌을 하고 n, p 두 입자가 나갈 때 중간자 π+가 interaction을 일으켰다고 봤는데, π+은 udbar가 공명된 상태를 본 것이다. 입자물리학자들은 실험데이터 점을 찍어서 피크의 폭으로 수명을 재고 높이로 에너지레벨을 재는 것이다. 중성자 양성자 산란실험이다. qqbar형태로 나타나는 것을 meson이라고 한다.
udu에서 u가 올라가다가 꺽여져서 시공에서 d와 dbar를 만들어낸다. 이를 쌍생성(pair generation)이라고 한다. 입자는 진공에서 생길 때 쌍생성된다. 이중 d는 그대로 올라가서 d가 되고, dbar는 옆으로 가서 다른 d입자가 올라오는 것과 만나서 쌍소멸(pair annihilation) 된다. 진공에서 그냥 생겼다 사라지는 것이다. 이때 올라오는 u와 쌍생성된 dbar가 공명상태 udbar가 된 것을 π+로 본 것이다.
반드시 쌍으로 생기고 사라진다. 왜 그런가 하면 Global gauge symmetry가 charge conservation을 하는데, 그 charge가 ‘electrical charge’, ‘weak charge’, ‘gluon color charge’ 이다. 이것을 보존해준다는 말이 반드시 입자와 반입자가 동시에 생기고 사라지는 것이다. Global gauge symmetry가 의미하는 것은 우주의 전기량은 반드시 보존되어야 한다는 것이다. 우주의 전하량이 바꾸지 않는다는 것으로 이것이 뇌터의 정리(Noether's theorem)이다.
일본이 1945년 원자폭탄이 터지고 잿더미가 되었다. 20만명이 원자폭탄에 죽고 참혹한 사건이다. 그 해 일본사람들이 일어날 수 있는 힘을 준 것이 1949년 노밸물리학상을 받은 유카와 히데키(湯川 秀樹, 1907~1981)이다. 완전히 참혹하게 전쟁에 진 상태에서 중간자 이론으로 일본인 최초로 노벨상을 받았다. 1935년 유카와 히데키가 quark에 대해서 모를 때 핵력은 중간자가 매개해 준 것이라는 발상을 최초로 해서 노벨상을 받는다. meson을 중간자로 번역했는데, meson은 qqbar형태의 결합이라고 1970년도부터 알게 된 것이다. 1950년대 사람은 꿈에도 생각 못 했던 이론이다. 그래서 모두 노벨상이 박혀있다.
meson을 드디어 알게 되었다. 시공상에서 짧게 묶여있는 것처럼 보이는 것이다. 이것을 커플링 되었다고 하고, virtual particle이라고 한다.
quark이 (u, c, t), (d, s, b) 6개이다. 구슬이 6개라 온갖 것을 만들 수 있다. 인간의 DNA에서는 A, G, C, T 4가지로 단백질 10만개가 나온다. 그런데 문자가 6개니 수백만 단어가 나올 수 있다. 그런데 우주를 만드는 법칙은 훨씬 간단하다. 왜 그렇게 수백만개를 안 만드느냐를 아는데 백년이 걸렸고, 그 이유가 군이론이다. 6개 쿼크로 문자를 만드는 법칙은 딱 2가지 밖에 없다. quark을 2개로 결합(qq)하든지, 3개로 결합(qqq)하든지 딱 2가지 법칙이다. 2개일 경우는 반드시 하나는 anti-quark이 온다. 2개로 모인 것은 스핀이 0 또는 1이 되어 보존역할을 한다. 그래서 힘을 실어 나른다. 3개일 경우는 6개가 다 들어와도 되나 t는 거의 없다. b도 희귀하다. 에너지는 무지하게 크지만 수명이 10-22으로 무지하게 짧기 때문에 들어와도 소용없다. 금방 사라진다. 그래서 u, c, d, s 4개만 따져주면 된다. u, d가 90%이고, c, s가 10%이다. qqbar를 meson이라고 하고, qqq를 baryon이라고 하고, 2개를 합쳐서 hadron이라고 한다. 우리가 모르는 것은 이름을 모르는 것이다.
딱 알아야 할 것은 이 그림이다. u가 와서 u로 안 바뀐 것을 ‘flavor unchange’라고 한다. flavor는 (u, c, t), (d, s, b)로 부르는 것이다. color와 구별된다. “u <-> d”는 flavor change라고 한다. “u <-> u”는 flavor unchange이고 color는 change 될 수 있다. Color octet이고 전부 묶는 이야기이다.
모든 학문의 끝에 입자물리학이 와 있다. 굉장히 좁은데 굉장히 높다. 여기 올라가서 보면 유기화학, 생화학 모두 보일 수 있다. 물리학과, 생물학과 다니는 것 아닌데, 만약 한 달 시간에 양자역학 돌파하라면 어렵다. 1년 걸린다. 그런데 한 달 주고 입자물리학 하라면 할 수 있다. 계약을 맺으면 된다. 암기하면 된다. 알아야 할 것이 몇 개 없다. 기본적으로 암기만 하면 한 달이면 충분하다. 입자물리학 석사수준까지 올라간다. 하겠다는 구체적 실행은 지금까지 한 것 다 암기해야 한다. 생물학, 브레인은 이렇게 할 수 없다. 10년은 지나야 보인다. 그러나 입자물리학은 누구나 맨 땡에서 시작한다. 미분적분도 없고 더하기만 있고, 수식도 푸는 것이 아니고 수식 자체만 기억하면 된다. 다이아그램과 문자 밖에 없다.
오늘도 산책하면서 “singlet, doublet, triplet, quartet, octet, decuplet” 을 암송하였다. 이 이상 방법이 없다. 공부 30년 한 사람 이야기이다. 그것이 안 되서 안 되는 것이다. 간단한 단어를 암기하는 것이 아니고 singlet, octet이 가장 많이 나오니 신호등에서도 singlet, octet, 밥 먹으면서도 singlet, octet 암송한다. 다 아는 것이지만 아는 것과 몸에 베는 것은 다르다. 여러분이 안 되는 것은 대충 들어보고 이름 아는 것 가지고는 안된다. singlet에 사무쳐 봐야 한다. 여러분이 암기해야 할 것이 10개가 안된다. 그것을 앞으로 열흘 동안 다른 일 전폐하고 10개의 용어를 매일 1시간 동안 발음을 해보라.
“singlet이 무슨 말이지? 하나라는 말인데, 뭐가 하나지?” 질문이 나중에 쏟아진다. 하드론이 드러날 때는 singlet으로 드러난다. 이런 말이 툭 나온다. “color charge도 singlet이 있구나? color charge의 singlet이 뭘까? color charge의 octet이 뭘까? meson의 singlet이 뭘까? meson의 octet이 뭘까?” singlet, octet 두 단어만 알면 모든 다이아그램이 이 속에 다 있다.
인생에서 입자물리학은 한 달이면 끝난다. 그러면 에베레스트산 올라가 본 것이니 모든 학문에 자신을 갖게 되고 탑-다운으로 공부할 수 있다. 한 번도 그런 관문을 돌파 안 해봤기때문에 어렵다 하고, 모르겠다 하고, 졸고, 이렇게 된다. 이제는 한 번쯤 끊어봐야 한다.
#5
스티븐 호킹의 강의를 조금이라도 이해하려는 사람은 가장 기본적으로 알아야 하는 것이 파인만 다이아그램이다. 파인만 다이아그램을 모르면 아예 입자물리학에 들어갈 수 없다. 파인만 다이아그램을 다시 보여준다.
화살표 계산하는 것밖에 없다. 화살표가 뭔가? 툭 건드리면 답이 나와야 한다. 모멘텀이다. 모멘텀이 바뀐 것이다. 꼭지점에서 나오는 것은 포톤이 될 수 있다. u가 들어가서 u가 나온다. quark이 안 바뀐 것을 flavor unchange라고 한다. 전기가 0이기 때문이다. 이 과정을 계산할 수 있다. 이 다이아그램을 인류역사상 처음으로 만들어내고 계산한 사람이 리처드 파인만이다. 대단하다.
모든 정보는 시공의 꼭지점(vortex)에 있다. 이 포인트에서 모멘텀(P)이 바뀌었다. 들어가는 것은 p1, 나가는 것은 P3로 적는다. 꼭지점에서 나오는 것은 포톤, w, z입자, 글루온 다 포함할 수 있다. 꼭지점에 글루온이라면 a로 적고 인데스 μ를 적는다. a는 글루온의 종류이고, μ=1,2,3이다.
계산을 보여주면, ubar(P3)Cj†〔-(i/2)gsλμaγμ〕CiU(P1)이다. 나가는 쪽을 먼저 적으면 ubar(P3)이다. gluon은 P1에 관여된 것을 i, P3에 관여된 것을 j라고 적는다. color를 넣으면 나가는 쪽에 Cj†이다. †를 붙이면 행렬이라는 말이다. 다음에 -(i/2)gsλμaγμ 가 붙어서 color의 흐름이라고 보면 된다. gluon이 8종류이고 색깔로 구분한다. gluon이 갖는 색깔을 charge로 봐서 color charge라고 한다. 다음에 color charge 오퍼레이터 Ci가 온다. 패턴이 보이는가? Ψbar( )Ψ에서 Ψ를 C로 바꾼 것이다. 색깔흐름이다. 다음에 마무리에서 들어오는 up-quark의 모멘텀 U(P1)이 붙는다. Ψbar( )Ψ를 계산하는 학문이 입자물리학이다. ΨbarΨ는 확률이 되고, 사이에 γ가 들어 있으므로 시공의 확률의 흐름이 된다. 그 구조 그대로이다.
C1=r=(1 /0 /0)이다. 색깔(r,g,b)을 행렬로 표시한다. 이렇게 두는 것이 internal symmetry이다. C2=g=(0 /1 /0)이다. C3=b=(0/ 0/ 1)이다. C1†=(1 0 0)이다.
이 행렬을 수식에 넣으면 계산이 된다. Cj†λμaCi 를 먼저 계산하면,
Cj†λμaCi = Cj†(λ1ia /λ2ia /λ3ia) = λjia 이다. 행렬을 계산하면 숫자가 된다. 숫자가 스칼라이고, invarient하고 그것이 대칭이다. color에 대한 대칭을 수식으로 찾아낸 것이다. 그 숫자가 λjia가 된다.
양성자 원자핵에서 u, u, d 의 질량은 3% 밖에 안되고, 97%는 글루온과 quark의 상호작용에너지이다. 그 상호작용을 계산하는 것이다. u, d만 알고 97%를 모르면 아는 것이 아니다. 글루온과 quark의 상호작용이 SUC(3)이다. 그 color를 계산하는 것이다. 어떻게 계산하겠는가? 1930년대부터 60년대까지 진행된 어마어마한 이야기이다. 페르미는 interaction이 교차로 한 점이라고 생각했다. 그런데 점이 아니고 엄청난 interaction이 있다. gluon을 알게 되면서, 핵력은 포인트에서 만나는 것이 아니고 gluon이라는 바다에 떠도는 quark 조각배 사이의 관계라는 것을 알게 되었다. 조각배와 파도 사이의 관계가 강한상호작용의 핵심이다. color charge와 quark의 interaction이다. 그것을 짊어지는 수식이 Cj†λμaCi = Cj†(λ1ia /λ2ia /λ3ia) = λjia 이다. 어마어마한 이야기이다. 이것밖에 없다. 그리고 계산하는 것이다. 계산은 직업적으로 하는 사람들이 하도록 내버려두고 공식이 어떻게 나오는가만 알면 100% 끝난다.
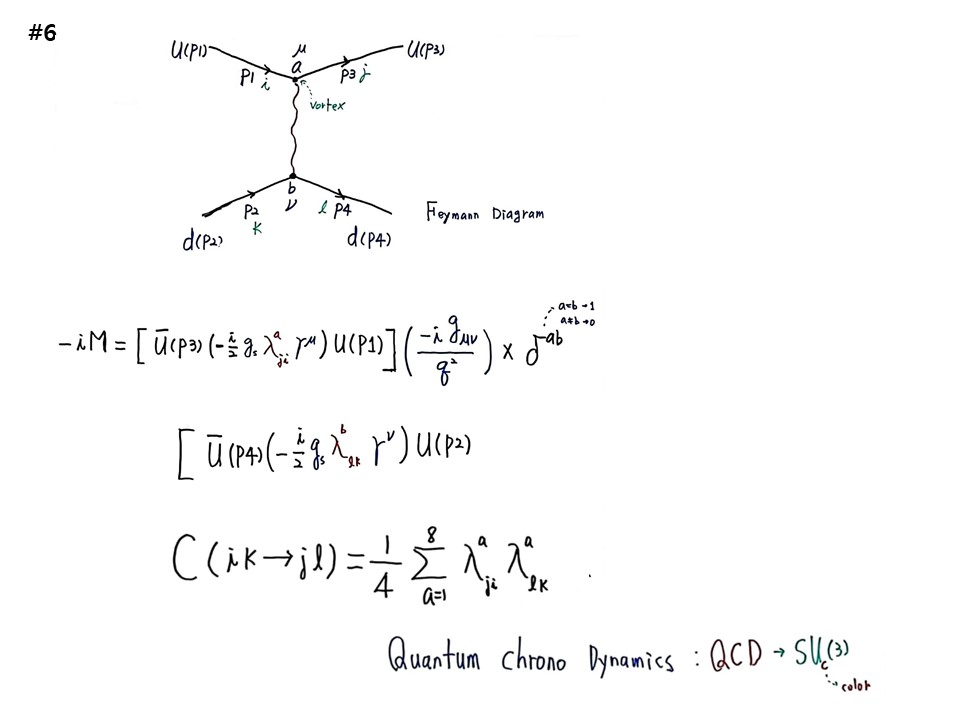
#6
다음의 파인만 다이아그램 계산은 P1, P3, P2, P4 벡터가 되고, u(P1)에서 u(P3)로 가고, d(P2)에서 d(P4)로 간다. color chage가 i, j, k, l이고, 위의 꼭지점이 a, μ, 아랫쪽 꼭지점이 b, ν이다.
u(P1)에서 u(P3)로 transition 확률을 계산하면 #5에서 계산한 값 Cj†λμaCi = λjia 를 집어 넣으면 〔ubar(P3)(-(i/2)gsλjiaγμ〕U(P1)이 된다. ubar(P3)와 U(P1) 사이의 흐름이다. quark가 color 바다가 엉겨붙어 일어나는 확률흐름이다. 3×3, λ 매트릭스 속에 다 들어있다. λ 매트릭스 8개 암기해야 한다.
다음은 a~b를 계산하여야 한다. 파인만의 계산결과는 –igμν/q2이다. 이때 q는 P3-P1의 모멘텀 차이다.
다음은 d(P2)에서 d(P4)로 가는 흐름은 〔dbar(P4)(-(i/2)gsλikbγν〕d(P2)가 된다. 그리고 수학적으로 ×δab를 적어주면 a=b라는 말이다.
그러면 계산결과는 C(ik->jl)=1/4 ∑a=18 λjia λika 가 된다. 이것을 계산해 주면 color charge의 전체 interaction을 알 수 있다. Quark과 Gluon의 interaction을 계산하는 학문을 Quantum Chrono Dynamics (QCD)라고 한다. 이것이 SUC(3)이고 C가 color이다.
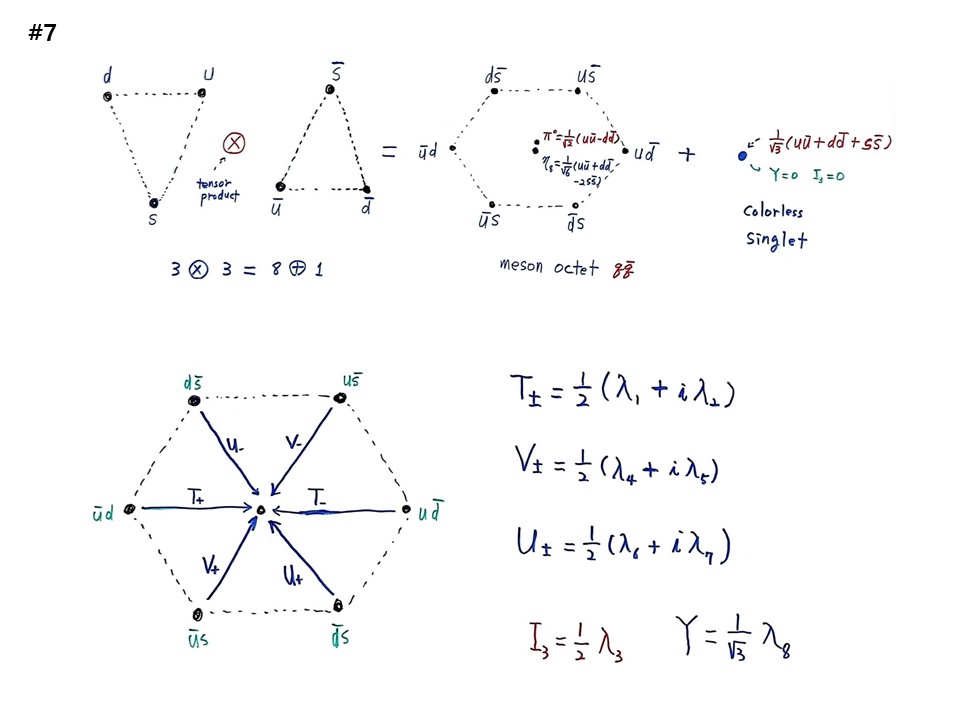
#7
모든 것이 삼각형 2개로 끝난다. quark model의 하이라이트이다. 점 3개를 찍고 점선을 연결하여 역삼각형이 되고 d, u, s 3가지를 적는다. 다른 점은 뒤집어서 반물질이 되면서 sbar, ubar, dbar가 된다. 다음은 텐서플로(TensorFlow)이다. AI의 핵심이다. 텐서곱tensor product)이라고 한다. 그러면 8개 점인 육각형이 나온다. dsbar, usbar 가 나오면서 meson 8중항이 된다. meson 8중항의 뿌리를 알게 된다. d, u, s 와 antiquark의 텐서곱을 하여 나온 것이다.
8중항의 가운데에는 2개가 있다. 그래서 8개이다. 첫 번째는 π0=(1/√2)(uubar – ddbar)가 계산결과로 나온다. 두 번째는 η8=(1/√6)(uubar + ddbar – 2ssbar)가 계산결과로 나온다. 엄밀한 계산이다. 여기까지 meson octet으로 qqbar로 되어 있다.
또 다른 하나가 singlet으로 나온다. (1/√3)(uubar + ddbar + ssbar)으로 계산된다. color는 없으므로 colorless singlet 이라고 한다.
그래서 3 ⊗ 3 = 8 ⊕ 1 형태로 나온다. 이것이 군이론(group theory)이다. 리, 킬링이 했던 쪽이다. 이것이 자연의 숨은 패턴이다. 3⊗3에서 9개의 상태가 나오는데 군이론에서는 8개와 1개로 갈라져야한다는 것이다. 실재로 찾아봤더니 octet+singlet으로 나온다. 기가 막히다. meson octet이 중요하다. 그래서 π입자, k입자 모두 1950년대 노벨상을 받았다. 당시 핫이슈였다. k입자를 따라가면 parity 이야기가 나온다.
8중항에서 3개의 quark사이의 변환과정을 군이론을 통해 다 알게 되었다. 관계가 계산이 되는 오퍼레이터를 찾아냈다. ubard에서 가운데로 가는 오퍼레이터가 T+이고, udbar 에서 가운데로 가는 오퍼레이터가 T-이다. 다음으로 ubars에서 가운데로 가는 오퍼레이터가 V+이고, usbar에서 가운데로 가는 오퍼레이터가 V-이다. 다음으로 dsbar에서 가운데로 가는 오퍼레이터가 U-이고, dsbar에서 가운데로 가는 오퍼레이터가 U+이다.
T±=1/2(λ1+iλ2), V±=1/2(λ4+iλ5), U±=1/2(λ6+iλ7)이 된다. 여기서 겔만매트릭스가 6개 들어갔다. 나머지 2개는 isospin I3=1/2λ3과 hypercharge Y=1/√3λ8 과 관계된다.
통째로 암기하라. 계역을 맺었다. 다 암기하면 패턴이 보인다.
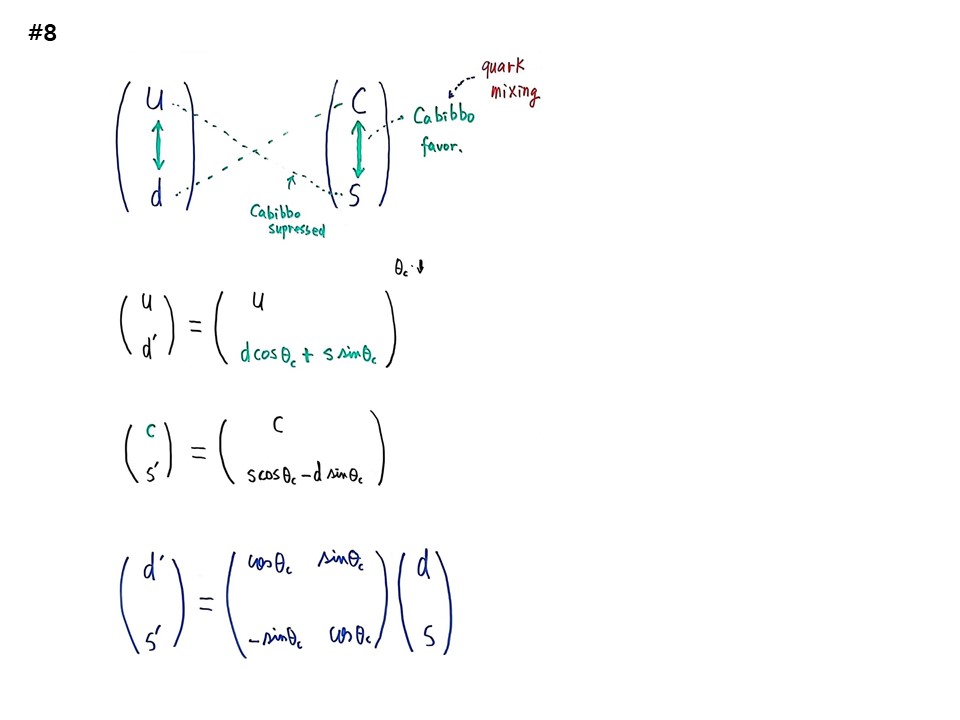
#8
u와 d의 관계를 추적하다가 1970년도에 이렇게 적을 수 있다는 것을 알게 되었다. (u d), (c S)가 묶이는데, (u <-> d), (c <-> s)는 잘 바뀌는데 u와 s, c와 d는 잘 안바뀐다. 이것을 처음 제안한 학자가 카비보(Nicola Cabibbo, 1935–2010)이다. 서로 안바뀌는 것을 Cabibbo suppressed라고 한다. 잘 바뀌는 것은 Cabibbo favoured이다. 그래서 카비보가 제안한 것이 d = d cosΘc +s sinΘc 로 추측을 해 보았다. 말이 되는 것이 Θc가 매우 작다. 그래서 sinΘc 는 0에 가깝고 cosΘc 는 1에 가까워 d’=d가 된다. 그래서 d‘은 d의 영향을 받지 s의 영향은 적다고 표현한다. 그래서 (c s’)으로 c라는 charm quark을 처음으로 개념상 제안한다. s’=s cosΘc - d sinΘc 로 표현할 수 있지 않은가로 시작하였다.
두 개념을 제안하고 묶어서 나온 것이 (d’ s’)=(cosΘc sinΘc / -sinΘc cosΘc)(d s)로 적을 수 있다는 것이다. 이것으로 중성류(Z0)를 예측한다. weak force의 비밀을 밝히는 단서를 11월 혁명 이전에 charm quark을 가정하기 시작했다. 카비보가 처음으로 가지고 있는 개념이 quark의 mixing 상태이다.
#9
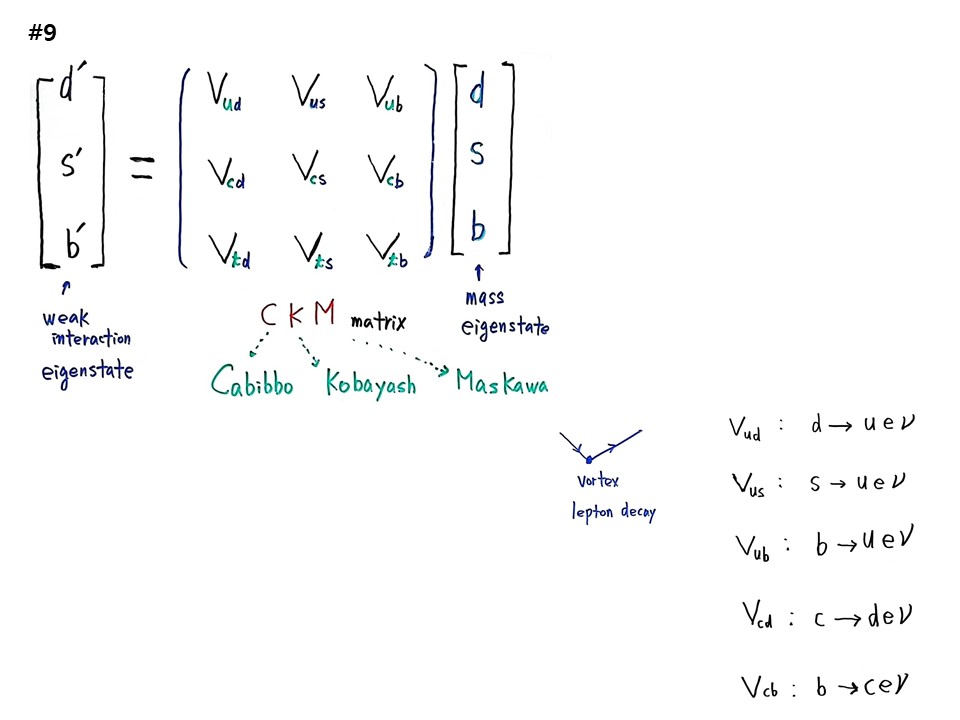
다음이 CKM 행렬이다. Cabibbo-Kobayash-Maskawa이다.
〔d’ / s’ / b’〕 = 〔Vud Vus Vub / Vcd Vcs Vcb / Vtd Vts Vyb 〕〔d / s/ b〕
〔d’ / s’ / b’〕는 weak interaction eigenstate이고 〔d / s/ b〕는 mass eigenstate이다.
Vortex에서 lepton이 decay 되는 것을 이 행렬이 설명한다. 질량이 높은 것에서 낮은 것으로 붕괴한다. Vud는 d가 붕괴되면 u,e,ν가 나온다. Vus는 s가 붕괴하면서 u,e,ν가 나온다. Vub는 b가 붕괴하면서 u,e,ν가 나온다. Vcd는 c가 붕괴하면서 d,e,ν가 나온다. Vcb는 b가 붕괴하면서 c,e,ν가 나온다.
#10
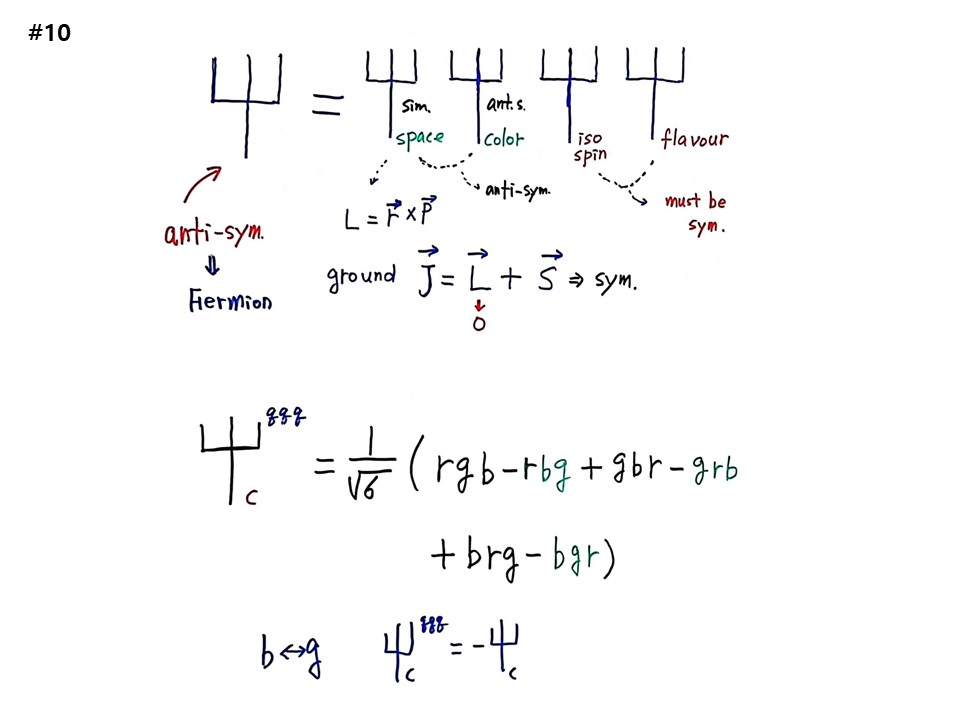
다음 시간을 위해 암기해야 할 것이 있다. 입자물리학에서 다루는 상태함수는 4개의 상태함수의 곱으로 되어있다. 최종결론이다.
Ψ=ΨspaceΨcolorΨisospinΨflavour 로 표시한다.
space는 L=r->×p->이다. r은 반지름 공간좌표이다. 입자물리학의 ground 상태에서는 total angular momentum J는 궤도각운동량 L과 스핀각운동량 S를 더해주는 것 J->=L->+S-> 이다. ground 상태에서는 L=0이므로 S만 따져준다.
color는 baryon의 color Ψcqqq=(1/√6)(rgb-rbg+gbr-grb+brg-bgr)로 적는다. b와 g를 바꾸면 Ψcqqq=-Ψc가 된다. 이 말은 color에 대해서 baryon은 anti-symmetry이다. space에 대해서는 symmetry이다. 그래서 space와 color를 곱한 값은 anti-symmetry가 된다.
baryon은 물질을 구성하는 fermion 입자이므로 결론적으로 anti-symmetry가 되어야 한다. 그래서 space와 color를 곱한 값은 anti-symmetry가 되므로, 나머지 isospin과 flavour는 반드시 symmetry가 되어야 한다. 이것이 어마어마한 이야기이다. Baryon의 Ω입자 sss가 anti-symmetry가 안되어 존재할 수 없는데, 왜 존재하게 됐는가를 설명하기 위해 만들어낸 것이 color charge의 출현이다.
Space는 symmetry이다. Color는 상황에 따라 다르다. qqq에서는 anti-symmetry로 결론이 났다. 그러면 나머지 isospin과 flavour를 곱한 값이 symmetry가 되어야 전체 값이 anti-symmetry가 된다. 그래야 페르미온이 된다. 그래서 파울리 배타원리가 얼마나 중요한가? 입자물리학에서도 마지막 가이드라인은 “페르미온인가 보존인가?”, “symmetry를 따르는가, anti-symmetry를 따르는가?” 이다.



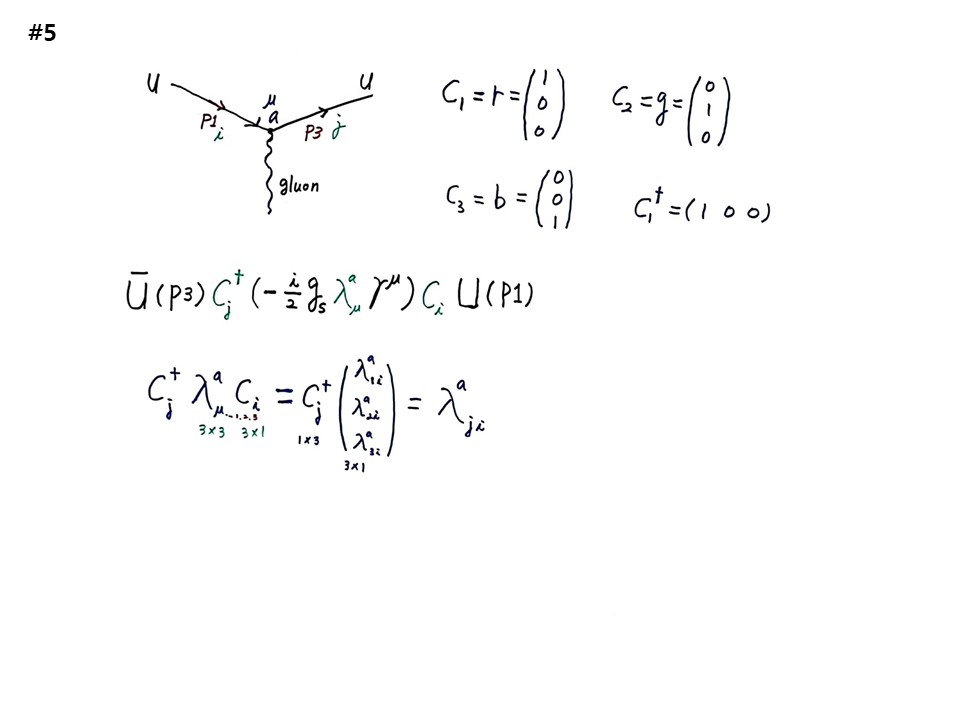
감사합니다! 복습에 큰도움이됩니다!