수업후기
#4
다음은 Rμν-1/2gμνR를 유도해야 한다.
Tμν=σC2〔1, β1, β2, β3/ β1, β1β1, β1β2, β1β3/ β2, β2β1, β2β2, β2β3/ β3, β3β1, β3β2, β3β3〕
이때 βi=vi/c 이다. 광속과 속도의 비로 둔다.
시간성분 T00=σC2 이 되어 E=mC2 과 같은 꼴이다.
중력장방정식을 적어보면.
Rμν-1/2gμνR=(8πG/C4)Tμν
아인슈타인은 물질텐서 Tμν가 발산이 0라는 확신을 갖고 있었다. 발산이 0이므로 보존이 된다. 그러나 Rμν로는 보존이 안되어, Rμν-1/2gμνR를 찾아냈다. Tμν가 발산이 0라는 것을 보여주어야 한다. Tμν를 ν에 대해서 공변미분(Tμν;ν)해보면 된다.
Tμν = σuμuν 로 적을 수 있으므로,
Tμν;ν = (σuμuν);ν =〔uμ(σuν)〕;ν = uμ;ν(σuν) + uμ(σuν);ν
(σuν);ν = 0가 되므로, u;νμ(σuν) =0임을 증명해야 한다.
σ는 밀도로 상수이므로, uνu;νμ=0 이 되어야 한다.
gμνuμuν=uνuν=1 이 된다. (uνuν는 스칼라가 되고 값이 1이다.)
(uμuν);ν=uiνμuν+uμu;νν=0가 된다. (스칼라값의 공변미분이므로 0임을 안다)
u;νν=0 이므로, uiνμuν=0이 되어야 한다.
따라서 uνuiνμ=uν(uiνμ+⌈ναμuα) = (dxν/ds)〔(duμ/dxν)+⌈ανμ(dxα/ds)〕 =0 가 된다.
정리하면, (duμ/ds) +⌈ανμ(dxα/ds)(dxν/ds) = 0
측지선방정식이 유도되었다. 두 가지로 유도되었다. 앞에서는 모멘텀의 평행이동으로 유도하였고, 이것은 물질에너지 텐서의 발산이 0가 되어야 한다는 원리하에 유도되었다.
측지선방정식이 뉴턴방정식에서 나온다. 그래서 아인슈타인방정식이 뉴턴방정식을 품고 있다는 것이다. 물리학이 대단하고 아름다운 것이다. (duμ/ds) 이 F=ma의 관성력이고, ⌈ανμ(dxα/ds)(dxν/ds)이 중력이다. 중력과 관성력이 등가가 되는 포인트이다. 정확하게 어디냐 하면 엘리베이터 타고 내려가다가 줄이 끊어졌을 때 사건이다. 이때 무중력이 되는데 이때 =0 이다. 비행기가 자유낙하하면 비행기 안에 사람이 붕 뜬다. 나를 당기는 힘이 없다는 것으로 무중력이다. 가속하는 힘과 중력이 = 이 되는 공식이다. =0가 되기 때문에 힘을 느끼지 않는다. 어마어마한 공식이다.
#5
물리학 15년 동안 강의한 것을 수첩 2페이지에 담았다. 가능하다. 공부에는 끝이 있다. 특히 물리학은 끝이 있다. 물리학은 올해 강의 8회가 끝이다. 입자물리학 뒷부분 남은 것이 있지만, 여기까지만 해도 물리학과 석사과정 끝난 것이다. 압축이 아니고 그대로 2페이지 밖에 아니다. 그 외에 없다. 물리학은 석사과정까지 99% 끝났다. 말이 과장이 아니다. 이 강의를 15년간 10회 평균하여 150주 했다. 1회당 4시간 600시간이다. 석박사 공부 600시간 하지 않는다. 미니멈 3배 이상 공부한 것이다. 여러분은 적어도 학부 졸업할 정도의 시간의 강의를 와서 들었다. 그러면 여러분과 나에게 각각 책임이 있다.
자연과학 지식의 최정점이 중력장방정식이다. 거의 90% 했다. 문제 푸는 것이 있는데 여기서는 할 필요 없다. 기본 백본구조는 90% 다 했다. 뭘 했는가를 알아야 한다. 제발 황당한 이야기 하지 말고 수식으로 보여달라고 하라. 박자세는 수식으로 쓰지 않는 것은 인정 안 하는 단체이다.
아인슈타인이 접근한 것은 물질텐서로 먼저 접근했다. 기호를 , 적는 것은 편미분(∂/∂x)이고, ; 적는 것은 공변미분(Dμ)이다. 공변미분한 Tμν;ν =0 라는 것을 아인슈타인이 알았다. 첫 발상은 전자기장에서 왔다. 자석에 철가루를 뿌리면 선이 나온다. 역장, Field라고 한다. 필드는 스칼라이다. 자석 주위의 공간은 힘을 받는데, 그것이 Force이다. 철가루가 움직이는 것이 측지선방정식이다. 그래서 자석이 있으면 전자기장이 있듯이, 물질이 있으면 물질에 영향 받는 공간이 생길 것이고, 그 공간은 4차원 시공일 것이라는 생각이 떠올랐다. 바위덩어리 Tμν가 있으면, 바위덩어리에 의해 주위의 시공이 달라질 것이다. 달라지면 곡면이 생길 것이라 하여 곡률 Rμν로 했는데, 이것이 리치텐서이다. 그런데 발산이 0가 아니라 좌절을 하면서 0가 되는 식을 유도하는 과정이 몇 년 걸린 것이다. 아인슈타인은 어마어마하게 고생핬는데 우리는 결과를 아니 그냥 따라가면 된다. 매끌하다.
수학자 비앙키(Luigi Bianchi, 1856-1928)가 항상 맞는 방정식을 유도했는데 ‘비앙키항등식’이다. 50년전에 유도한 이 방정식을 아인슈타인이 몰랐다. 자기 혼자 끙끙거리고 유도하고 봤더니 이미 있었던 것이다. 이중으로 증명이 된 것이다. 비앙키항등식을 유도하고 축약해서 1/2gμνR을 찾아낸 것이다.
비앙키항등식 암기하여야 한다. Rαμ는 고정되고 ρσ;ν가 한 개씩 밀어내면서 순서가 바뀐다.
Rαμρσ;ν + Rαμσν;ρ + Rαμνρ;σ = 0 가 됨을 비앙키가 증명을 했다.
어떤 양을 시간에 대해서 미분했는데 0가 된다는 것은 그 양이 시간에 대해서 안 바뀐다는 것으로 에너지보존의 법칙이다. 마찬가지로 어떤 양을 공변미분해서 0라는 것은 그 양이 상수라는 말이다.
다음은 매트릭텐서 gμρ를 곱하고, 인덱스 ν -> α 로 바꾸어준다. 우리는 답을 아니까 바로 하지만, 모르는 상황에서는 날 샌다. 머리 다 빠진다. 아인슈타인이 여기서 편지를 보냈는데, “내가 특수상대성 유도할 때는 수학자를 얕보았는데, 지금 이 공식을 유도하는 과정에서 수학자가 존경스럽다”고 하였다.
gμρ(Rαμρσ;α + Rαμσα;ρ + Rαμαρ;σ) = 0
첫 번째, gμρRαμρσ = gμρRασμρ (μρσ -> -ρσμ -> σμρ 로 3번 로테이션 하였다.
그러면 μρ가 약분되어, Rασ 가 된다. 이것을 인덱스 축약이라고 한다.)
두 번째, gμρRαμσα = gμρRμσ = Rρσ
세 번째, gμρRαμαρ = -gμρRαμρα = -gμρRμρ = -R (스칼라곡률로 나온다)
계산한 것을 넣으면,
Rασ;α + Rρσ;ρ - R;σ = 0
(ρ->α로 바꾸면)
2Rασ;α - R;σ = 0
(;σ -> ;α 로 바꾸기 위해 δ함수를 넣어주면)
Rασ;α - (1/2)δασR;α = 0
(Rασ - (1/2)δασR);α = 0
(gρσ를 곱해주면)
〔gρσRασ - (1/2)δασgρσR〕;α = 0
〔Rρα - (1/2)gραR〕;α = 0
(ρα -> μν로 버꾸어주면)
〔Rμν - (1/2)gμνR〕;α = 0
공변미분이 0가 되므로, Rμν - (1/2)gμνR 양은 보존이 된다. 그래서 Rμν - (1/2)gμνR을 아인슈타인 텐서라고 하고 약자로 Gμν라고 적는다.
따라서 Gμν=KTμν 가 일반상대성 공식이 된다. 중력장방정식 골격은 다 끝났다.
#6
물리학은 이것 밖에 없다. 오늘 새벽에 수첩 2페이지로 적은 것이다. 2페이지로 줄인 것이 아니고 물리학을 아무리 적어봐도 2페이지 이상 없다는 것을 알게 된다. 이제 희망이 보인다. 무조건 아는체 하라.
첫 번째 중력(G)이다.
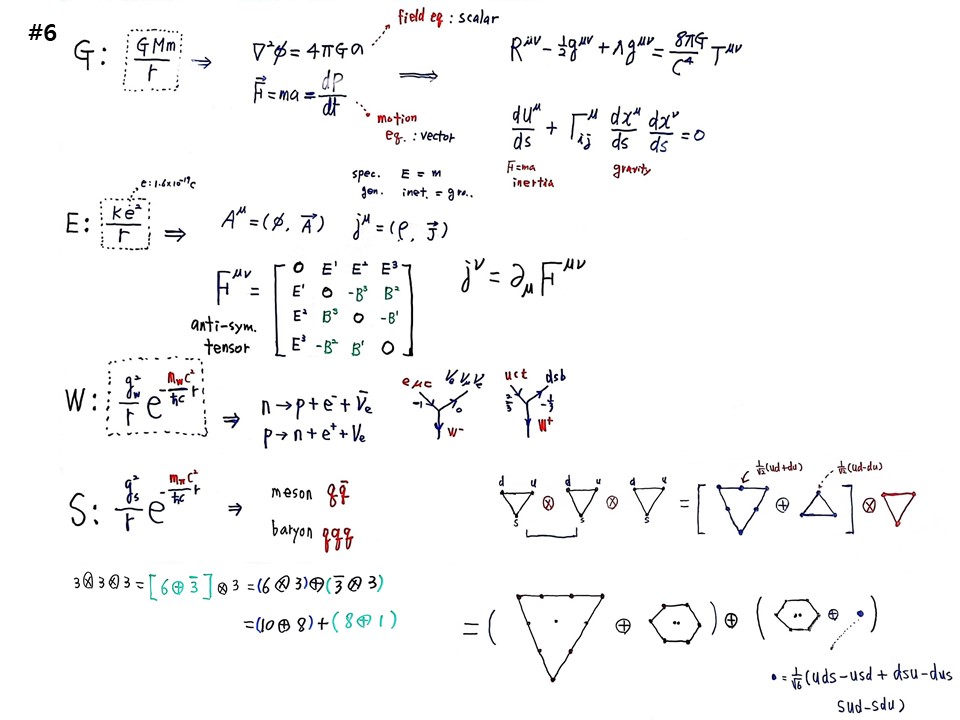
중력의 포텐셜에너지는 중력장 GMm/r 이다. 뉴턴의 장방정식(Field equation, scalar)은 푸와송방정식 ▽2Φ=4πGρ 이다. ρ는 밀도이다. 뉴턴의 운동방정식(Motion equation, vector)은 F=ma=dP/dt이다. 장은 바다, 힘은 파도이다. 모두 이렇게 되어 있다. 우주의 4가지 힘에 대해서, 중력장이라는 바다에서 파도가 일어난 것이 중력, 힘이다. 파도가 나에게 쳤다. 나한테 왔으니 방향이 있고 벡터이다. 바다는 방향이 없으니 스칼라이다. 이것은 3차원 버전이다.
4차원 버전으로 쓰면, 장방정식이 아인슈타인의 중력장방정식 Rμν - (1/2)gμνR + ⋀gμν = (8πG/C4)Tμν 이다. 전부 스칼라량, 엄밀히는 텐서량이다. 스칼라량도 텐서량의 부분집합이다. 텐서량이면 어딜 가도 틀릴 수가 없다. 4차원 운동방정식은 측지선방정식 (duμ/ds) + ⌈ljμ(uiuj) = 0 이다. 우주의 모든 움직이는 물질은 가속도와 중력의 등가원리가 되는 골짜기를 따라 이동한다는 것이다. 그것이 다른 말로 최단거리를 간다는 것이다. (duμ/ds)는 F=ma에 해당되고 관성력(inertial force)이다. ⌈ljμ(uiuj)이 중력(gravity)이다..
관성력 개념이 어렵다. 초속 100km로 가는 인공위성에서 죽은 사람의 관을 초속 50km로 우주 바깥에 버린다면, 인공위성을 귀신처럼 따라올 것이다. 상식으로 안 느껴진다. 초속 100km로 가는 인공위성에서 권총을 반대로 초속 50km로 쏘면, 다시 와서 충돌한다. 놀랍다. 아직 우리는 관성을 모른다. 버스 타다가 브레이크 잡으면 앞으로 와서 넘어지는 것과 버스를 수직으로 놓으면 엘리베이터가 되는데 엘리베이터 줄이 끊어지는 것과 같다. 이쪽 공부는 사고실험을 엄청해야 한다. 관성력과 중력이 정확하게 같아지면 힘을 못 느낀다. 이를 자유낙하라고 한다. 엘리베이터가 떨어지는 것이 자유낙하이다. 자유낙하는 힘을 못 느낀다는 핵심이다.
특수상대성 이론은 에너지(E)와 질량(m)이 같다는 것이다. 일반상대성 이론은 관성력(inertial force)과 중력(gravity)이 같다는 것이다. 이것을 수식으로 바꾸어 놓은 것이다. 우리는 지구표면에 살기 때문에 이해가 안된다.
두 번째 전자기력(E)이다.
포텐셜은 ke2/r 이다. e는 전하량(electrical charge)으로 1.6×10-19 쿨롱(C) 이다. 전하량 e은 커플링계수이다. 그래서 GMm/r에서 질량도 어떤 측면에서는 커플링계수이다. 분모에 r이 있으니 field로 전자기장이다. 4차원 벡터 Aμ의 시간성분 Φ가 스칼라포텐셜로 전압(voltage)과 관계된다. 공간성분은 벡터로 A->로 나온다. 따라서 Aμ=(Φ, A->)이다. 쌍으로 있는 것이 jμ=(ρ, J->)로 적는데, ρ는 전하(charge)로 시간상 존재하는 것이고, J->는 전류(current)로 공간상 움직이는 것이다. 정전하와 전류를 4차원 버전으로 한꺼번에 적은 것이다.
필드에 해당하는 것이 Fμν 텐서인데 맥스웰방정식을 유도할 수 있다.
Fμν=〔0 E1 E2 E3 / E1 0 -B3 B2 / E2 B3 0 -B1 / E3 -B2 B1 0〕
이것이 반대칭텐서(anti-symmetry tensor)이다. 따라서 맥스웰방정식은 jν=∂μFμν 로 적는다.
세 번째 약력(W)이다.
여기의 바다 Weak field는 (gw2/r)e-(mwC2/ħC)r 이다. gw는 약력의 커플링계수로 원자핵 속에 있으므로 멀리 못가고 급격히 감소한다. 그래서 감소하는 팩터가 e-(mwC2/ħC)r이다. mw=80GeV이다. 굉장히 큰 값이라 r이 조금만 가도 0로 떨어진다. 그래서 핵력은 멀리 못 간다. 여기에서 n->P+e-+νebar 인 베타붕괴가 나온다. 베타붕괴는 주기율표 할아버지이다. Lepton은 전하량 –1인 입자 e, μ, τ 에서 w-가 빠져 나오면서 전하량 0인 νe, νμ, ντ 로 바뀐다. Quark은 전하량 2/3인 입자 u, c, t 에서 w+가 빠져 나오면서 전하량 –1/3인 d, s, b 로 바뀐다.
네 번째 강력(S)이다.
여기의 바다 Strong field는 (gs2/r)e-(mπC2/ħC)r 이다. 여기서도 지수함수로 감소하므로 핵 바깥으로 가면 없어진다. meson은 qqbar, baryon은 qqq로 만들어진다. 여기서는 집합론이다.
u, d, s로 역삼각형을 만들어주고 텐서곱을 한다. 스칼라도 텐서고, 벡터도 텐서이다. 물리학 방정식이 텐서로 표시되면 공변성을 갖게 되고 틀릴 수 없다고 한다. 중력장방정식이 텐서방정식이다. 텐서곱은 ⊗로 표시한다. 역삼각형 3개를 텐서곱을 해주면 묘하다. 텐서곱의 결과는 3⊗3⊗3=〔6⊕3bar〕⊗3=(6⊗3)⊕(3bar⊗3)=(10⊕8)+(8⊕1)이 된다. (10⊕8)은 10중항과 8중항으로 나뉜다. (8⊕1)은 8중항과 1중항으로 나뉜다. 자연이 집합론을 따른다.
다이아그램으로 그리면, 역삼각형 3개를 텐서곱을 해주면 앞에 2개를 먼저 곱하면, 6중항 역삼각형과 3중항 반물질 삼각형이 나오고 이를 뒤의 3중항으로 곱해준다. 6중항 역삼각형과 3중항 역삼각형을 곱하면 10중항(Baryon decuplet)과 8중항(meson octet)이 나온다. 삼각형 3중항과 역삼각형 3중항을 곱하면 8중항(octet)과 1중항(singlet)이 나온다. 1중항은 (1/√6)(uds-usd+dsu-dus+sud-sdu)가 된다. 삼각형 포인트마다 다 계산할 수 있다.
#7
벡터 V와 W가 있다면, V.W=Scalar product로 결과는 숫자가 나온다. V×W=vector product로 결과는 vector가 나온다. V⊗W=tensor product로 결과는 tensor가 나온다.
상대성이론에서 광속도 C, 거리를 l로 보면, C=dl/dt이고, cdt=dl이다. 특수상대성에서 time-like, space-like, light-like 라고 한다. 원뿔 시공다이아그램에서 안에는 인과적으로 연결되고 바깥쪽은 연결 안된다고 하는 것으로 이때 45도선이 cdt=dl로 빛이 가는 선이다. 이 양을 제곱을 하면 (cdt)2-(dl)2=ds2으로 두었다. 따라서 ds2=c2dt2-dx2-dy2-dz2 이 되고, 행렬로 표시하면 (1×4)(4×4)(4×1)행렬로
(cdt dx dy dz)(1 0 0 0/ 0 –1 0 0/ 0 0 –1 0/ 0 0 0 –1)(cdt / dx / dy / dz)
=dxμgμνdxν=dxμdxμ가 된다.
dxμdxμ 변환을 로렌츠변환이라고 한다. 어깨에 인덱스 쓰는 것을 contra-varience(반변), 발목에 쓰는 것을 co-varience(공변)이라고 한다. 공변은 곡선에서 접선을 말하고, 반변은 법선을 말한다. 접선과 법선은 항상 90도로 텐서곱하면 1이 된다. 텐서량이므로 틀릴 수 없다. 따라서 dxμdxμ량은 불변량(invarience)이 된다. 어떤 좌표계에서도 통용되는 일정한 값을 갖는다. 지구든 달이든 상관이 없다.
물리학에서 공간에 관한 것이 있다. 파장이 줄어들면 에너지가 올라간다. 물리학에서 이것만 알면 다 풀린다. 1μm는 10-6m이다. 10-9m, 10-12m, 10-15m, 10-18m가 있으면 곧장 에너지와 연결된다. 태양에너지는 1eV이고 온도는 1만도이다. 1μm는 파장이 긴 태양빛으로 10-6m는 에너지로 1eV가 된다.
10-9m는 나노미터로 원자 사이즈로 KeV이다. 원자를 보려면 파장이 10-9m가 되어야 한다. 병원에서 흉부X선 파장이 KeV이다. 원자 사이즈를 보면서 허파의 윤곽이 나온다. 반도체 결정이나 재료공학에서도 X선을 쓰는데, 1~수십 KeV 단위이다. 온도로는 107=천만도로 핵융합이 일어날 수 있는 온도이다.
10-12m는 원자핵 속으로 들어가는 크기로 MeV이다. 방사선은 기본적으로 들어가는 크기가 10-12m이고, 원자핵을 건드리려면 최소 MeV가 되어야 한다. 온도로 바꾸면 1010=100억도이다. 전자가 60억도이다. 그래서 원자핵에서 나올 수 있다. 전자가 원자핵에서 나오는 것이 베타붕괴이다. 실재 와 닿는다. 온도를 eV로 바꾸는 것을 한 달간 연습하면 방사선, MRI, 암석, 세포, 별, 우주가 한꺼번에 이해가 된다. 핵속은 기본온도가 100억도이다. 지구상에서 아무도 건드릴 수 없다. 오직 별 속에서 일어난다. 그런데 지구에서도 국부적으로 일어난다. 베타붕괴이다.
10-15m는 GeV로 양성자이다. 109ev로 온도는 1013=10조도이다. 양성자의 질량을 온도로 바꾼 값이다. 함부로 양성자 이야기 하지마라. 양성자를 조사하려면 쏘는 입자의 에너지가 GeV가 되어야 친구가 될 수 있다. 갑자기 거인과 친구가 될 수 없다. 자기도 키가 그만해져야 한다.
w입자의 질량은 80GeV, top quark은 172GeV이다. 그래서 10-18m까지 들어가야 한다. TeV이다. quark 레벨의 이야기이다. Tevatron 이름이 여기에서 왔다. 온도는 1016=1경도이다.
우주자체의 온도는 γ-선이다. photon온도가 1013도 이상이 되면 포톤의 에너지에 의해 양성자 입자와 반입자가 생길 수 있다. 그런데 온도가 1013도 보다 떨어지면 양성자와 반양성자가 만나서 다시 포톤으로 되는 것이 많아진다. 1013도보다 높아지면 생기는 것과 없어지는 것이 균형을 이룬다. 열평형(Thermal equilibrium)이다. <태초의 3분간>에서 엄밀한 수식이 나왔던 것은 열평형 상태이기 때문이다. 그런데 온도가 떨어지는 10-6초 이후가 되면, 양성자와 반양성자가 만나서 다시 포톤으로 되는 것이 압도적으로 많아진다. 그러면 양성자가 생기는 것 보다 사라지는 것이 빨라진다. 쌍생성 할 때 양성자는 10억개+1개가 더 있었고, 반양성자는 10억개 있었다. 정물질이 왜 1개가 더 생겼는가는 우주론의 마지막 질문이다. 처음으로 힌트를 낸 사람이 노벨상 받은 러시아의 사하로프(Andrei Sakharov, 1921-1989)이다. 이때 나온 것이 ‘CP-비보존’이다. ‘CP-비보존’ 때문에 입자와 반입자가 생길 때 10억분의 1만큼 입자가 더 생긴다. 온도가 떨어져 10억개 쌍소멸 될 때 1개 남은 입자가 지금 여러분이다. 그것이 100만분의 1초에서 양성자가 생겼다는 말이다. 이때 생긴 양성자는 온도가 떨어지니 더 생기지는 않고 계속 남아 있는다. 오늘 강의 끝나고 <태초의 3분간> 찬찬히 읽어보면 다 이해될 것이다.




힘드셨죠.잘 보겠습니다.