수업후기
#10
그럼 어떻게 주기율표를 만드는가? 주기율표는 양자의 세계이다. 양자역학에서는 다음을 계산한다.
∫(L+Y)*(L+Y)dΩ
(L+Y)에서, L+ 는 오퍼레이터이고, Y는 슈뢰딩거방정식을 풀면 나오는 복잡한 전자의 파동방정식의 한 부분이다. 그 부분은 전자가 존재확률구름으로 나오는데, 가만있지 않고 바이브레이션하면서 축구공 껍질처럼 있는 것을 구면조화함수라고 하고, 반지름이 커졌다 작아졌다 한다. 우리가 아는 원자가 고정되어 있지 않고 확률구름이다. 확률구름이 축구공 껍질처럼 있는 것을 구면조화 Y라고 표시하고, 반지름(Radius)이 늘었다 줄었다 하는 것을 R로 표시한다. R은 계산이 복잡해서 따로 해야 한다. R이 늘었다 줄었다 하는 것은 위도Θ 와 경도Φ에 관한 것이다. 전자구름의 파동함수가 Y로 표시되는데, 그것에 대해서 L+ 오퍼레이터 하는 것이다. L+=Lx+iLy이므로 x방향의 각운동량을 계산한 것과 y방향의 각운동량을 복소공간에서 계산한 것을 더하라는 말이다.
(L+Y)* 는 (L+Y)의 conjugator이다. 복소수를 알아야 한다. 복소수 L+=Lx+iLy라면, conjugator를 하면, (L+)*=Lx-iLy가 되고 계산한 결과를 L-이라고 한다. (L+Y)*(L+Y)를 하면 다시 실수로 바꾸어 준다. 그래야 자연을 묘사할 수 있다.
∫(L+Y)*(L+Y)dΩ = ∫Y*L-L+YdΩ가 된다.
교환이 안되는 시스템이라 순서를 바꾸면 안된다.
L-L+ = (Lx-iLy)(Lx+iLy) = Lx2 + Ly2 + iLxLy – iLyLx 이다.
그러면, L2 = Lx2 + Ly2 + Lz2 이므로, Lx2 + Ly2 = L2 – Lz2 으로 ‘동어반복’이다. 이해하는 것이 아니다. 동일한 것 찾아 치환하는 것이다.
따라서 L-L+ = L2 – Lz2 + i〔Lx, Ly〕로 교환자가 된다. 양자역학은 교환자의 학문이다.
오퍼레이터가 양자화되면 〔Lx, Ly〕=iħLz가 되므로,
L-L+ = L2 – Lz2 - ħLz이 된다.
#11
따라서 ∫(L+Y)*(L+Y)dΩ = ∫Y*L-L+YdΩ
= ∫Y*(L2 – Lz2 - ħLz)Y dΩ 가 된다.
첫 번째 L2 이 Y에 작동하면 L2Yλm = λħ2Yλm에서 λħ2이 되고,
두 번째 Lz2 이 Y에 작동하면 Lz Ylm = mħYlm에서 두 번 한 것이기에 m2ħ2가 나온다.
세 번째 ħLz 이 Y에 작동하면 Lz 은 mħ인데, ħ가 또 있으므로 mħ2이 나온다.
따라서
= ∫Y*(λħ2 – m2ħ2 - mħ2)Y dΩ 가 된다.
또한 L+Ym=CYm+1 로 적을 수 있으므로,
∫(L+Ym)*(L+Ym) = CC*∫Ym+1Y*m+1 = │C│2이 된다.
따라서
∫Y*(λħ2 – m2ħ2 - mħ2)Y dΩ =│C│2∫Y*m+1Ym+1 dΩ가 되므로,
λħ2 – m2ħ2 - mħ2 =│C│2 ≥ 0 이고,
따라서 λ – m2 - m ≥ 0 가 된다.
이것을 풀면,
λ ≥ m2 + m
λ ≥ m(m+1) 이고,
등호(=)가 성립하려면 m이 최대값(max)을 가져야 하므로,
λ = mmax(mmax+1) 이 되어야 한다.
그래서 m의 max값을 새로 부르는 이름을 “l”이라고 했다. 이제 주기율표를 알 수 있게 되었다. l=0면 s궤도, l=1 이면 p궤도, l=2이면 d궤도, l=3이면 f궤도이다.
따라서 L2Yλm = λħ2Yλm에서 λ=l(l+1)값을 갖는다.
또한 Lz Ylm = mħYlm에서 m 값은 l=1이면 m은 -1, 0, +1이 된다.
출발이 l값이다. l값이 나오면 주기율표는 그냥 나온다. 고전물리학의 푸아송 괄호에서 각운동량에 대해 맹활약해서 나온 것이 l값이다. 여기서 쓴 것은 교환자이다. 교환자 방식이 아니면 못 푼다. 곱하기 밖에 안했다. 교대군인 두 오퍼레이터를 곱한 것이다. (A×B)-(B×A)가 0인 것이 ‘고전물리학’, 0가 아닌 것이 ‘양자역학’이다. 그 분기선을 본 것이다.
#12
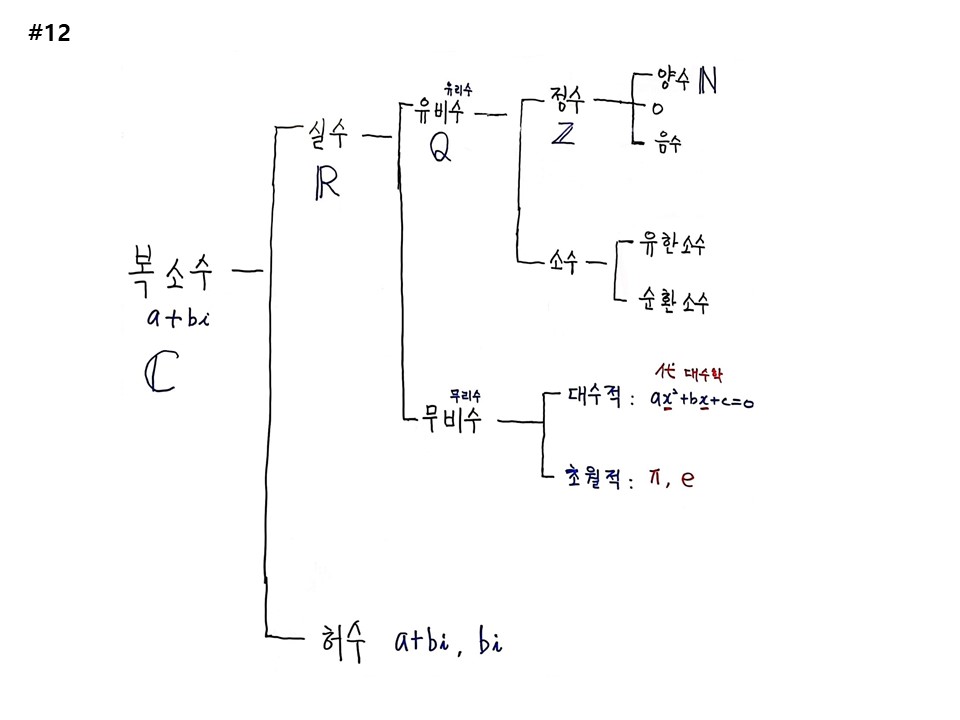
수 체계를 알아야 한다. 수 전체를 모르면 물리학을 할 수 없다.
수의 가장 큰 집합은 복소수이다. 복소수는 실수와 허수로 되어 있다. 실수는 비례로 표시할 수 있는 유비수(유리수), 비례로 표시되지 않는 무비수(무리수)가 있다. 유비수에는 정수와 소수가 있다. 정수는 양수, 0, 음수로 되어 있다. 소수는 두 가지가 있다. 유한소수와 순환소수이다. 무비수에는 ‘대수적 무비수’와 ‘초월적 무비수’로 나뉜다. 대수적이라는 말은 대수방정식에서 나왔다. 대수방정식은 ax2+bx+c=0의 형식으로 대수(代數)는 수를 바꾸어치기 한다는 뜻이다. 5차 대수방정식의 근이 없다는 것을 보여 준 사람이 갈루아이다. 대수방정식을 풀다가 대칭의 문을 열고 인류역사가 바뀌었다. 대수방정식에서 나오는 모든 수가 대수적 무비수이다. 초월적 무비수는 방정식 답에서 나온 값이 아니다. π, e가 대표적이다. 이외에도 초월적 수는 어마어마하게 많다. 다음에 허수가 있다. 허수는 두 가지이다. a+bi, 와 bi 형태이다.
집합론에서는 약자를 쓴다. 복소수는 C, 실수는 R, 유비수는 Q, 정수는 Z, 양수는 N이다.
#13
다음은 eix=cosx+isinx 를 뿌리 뽑는다. 이거 헷갈리면 물리학 공부 포기해야 한다. 보통 공학박사까지 하면서 가장 많이 만나는 수식이 ‘테일러 급수(Taylor series)’이다. 테일러 급수만 알면 모든 것이 다 풀린다. 알아야 할 것은 하나도 없다. ‘동어반복’ 밖에 없다.
미분가능한 연속함수 f(x)를 무한급수로 보겠다는 것이다. 그러면 다 풀린다. 인터뷰 기사에서 “어떻게 하면 수학을 잘 하느냐?” 물어보니, 필드상 받은 세계적 수학자들 사례에서 어린시절 엄마가 슈퍼마켓 가서 바나나 개수, 통조림 개수 헤아려 보라고 했다고 한다.
따라서 대칭을 맞추어 하나하나 헤어리며 최대한 길게 적어보는 것이 중요하다.
f(x)=a0x0+a1x1+a2x2+a3x3+a4x4+a5x5+a6x6+.....
1번 미분을 하면,
f’(x)=a1x0+2a2x1+3a3x2+4a4x3+5a5x4....
2번 미분하면,
f’‘(x)=1.2a2x0+2.3a3x1+3.4a4x2+4.5a5x3....
3번 미분하면,
f’‘’(x)=1.2.3a3x0+2.3.4a4x1+3.4.5a5x2....
f(0)=a0, f’(0)=a1, f’‘(0)=1.2a2, f’‘’(0)=1.2.3a3
패턴을 발견하라. f(4)(0)=1.2.3.4a4가 된다. 하나도 어렵지 않다.
이제 뒤집어서 적으면,
a0=f(0)/1, a1=f’(0)/1, a2=f’‘(0)/1.2, a3=f’‘’(0)/1.2.3, a4=f(4)(0)/1.2.3.4 가 되어.
1=0!, 1=1!, 1.2=2!, 1.2.3=3!, 1.2.3.4=4!로 적을 수 있다.
따라서 f(x)에 집어 넣으면,
f(x)=(f(0)/0!)x0+(f’(0)/1!)x1+(f’‘(0)/2!)x2+(f’‘’(0)/3!)x3+(f(4)(0)/4!)x4.....
이것이 수학사에 그 유명한 테일러 전개이다.
#14
테일러 전개로 첫 번째 응용을 하면,
함수가 eix일 경우, (eix)’=ieix, (eix)’‘=iieix=-eix,...
eix=(1/0!)x0+(i/1!)x1+(-1/2!)x2+(-i/3!)x3+(1/4!)x4+(i/5!)x5+(-1/6!)x6+....
실수와 허수를 분리하면,
eix=(1/0!)x0-(1/2!)x2+(1/4!)x4-(1/6!)x6+i〔(1/1!)x1-(1/3!)x3+(1/5!)x5+....〕
함수가 sin(x)일 경우, sin’ -> cos’ -> -sin‘ -> -cos ... 이 된다. sin(0)=0, cos(0)=1이므로,
sin(x)=(0/0!)x0+(1/1!)x1+(-0/2!)x2+(-1/3!)x3...= (1/1!)x1-(1/3!)x3+(1/5)x5...가 되어,
eix전개의 허수 부분과 일치한다.
마찬가지로 cos(x)의 전개는 eix전개의 실수 부분과 일치하므로,
eix=cosx+isinx가 된다.
위 식에 x=π/2를 넣으면,
ei(π/2)=cos(π/2)+isin(π/2)=i가 된다.
양변에 i승을 하면,
(ei(π/2))i=(eii(π/2))=(e-(π/2))=(1/(e(π/2))=0.207... =(i)i 이 된다.
(i)i 은 그림자에 그림자 승을 한 것이다. 그런데 그 값이 0.207... 의 실수가 나온다. 왜 우리가 수학을 해야 하는가? 허수는 존재하지 않는 귀신처럼 느꼈으나 허수의 허수승을 하니 실수가 나온 것이다. 꿈 꾸다 백만장자가 되었는데, 꿈 깨니 백만장자 그대로 된 것이다. ’그림자의 꿈‘이 실재세계를 만들어 버린다. 숨이 막힐 정도로 놀랍다. 이번 강의를 따라오는 것은 일체 공부하는 것이 아니라는 것을 깨닫는 것이다.
#15
양자역학과 입자물리학이 왜 생겼는지? 수학사를 하지 않으면 못 따라온다. 아벨에서 갈루아, 조르당, 리, 킬링으로 가는 과정이다. 킬링에 가면 SU(3)×SU(2)×U(1)이 만들어진다. 이것을 다른 말로 우주전체이다. SU(3)는 ’uud <-> ddu‘로 되는 과정으로, 치환이라고 적고 대칭이라고 읽으면 된다. SU(2)는 전자(e-)와 뉴트리노(νμ)를 치환한다. 킬링의 로테이션을 이해하려면 아벨에서부터 수학사 전체를 이해해야 한다.
갈루아는 다항식의 해이다. 5차 방정식의 해는 5!=120개이다. 120개를 치환하려면 머리가 다 빠진다. 몇 년간 거품물고 넘어져야 한다. 갈루아는 그걸 했던 사람이다. 120가지 해를 부분군으로 나누어서 최종부분군이 Normal-subgroup인 ’자가동형치환‘이 존재하느냐이다. 내가 메인구조를 유지하고 있는 최극단이다. 정규 Normal-subgroup이 존재하지 않는다고 정의하면 내가 다른 사람이 되어 경계를 넘어가 버린다. 갈루아는 A5 교환군 120가지 중 60가지는 정규 Normal-subgroup이 존재하지 않는다고 증명했다.
조르당은 3차원 공간의 선형변환으로 바꾸었다. 여기서부터 행렬이 나온다.
리는 이를 원운동으로 바꾸었다. 원의 접선은 무한개이다. 이 말 속에 다 있다. 접선은 미분이다. 대수방정식을 접선을 구하는 미분방정식로 바꾸었다. ’무한소‘라는 개념이 여기서 나온다. 무한소의 오퍼레이터의 다른 이름이 연속대칭이다. 무한소가 나오면 반드시 에너지, 물질, 시간을 설명하는 방정식이 되고, 그것이 운동방정식이다.
킬링은 분류를 해서 5가지가 나오는데 그 중 하나가 SU이다. SU까지 따라와야 8번 강의 끝나면 입자물리학이 그대로 옮겨감을 알 수 있다.
#16
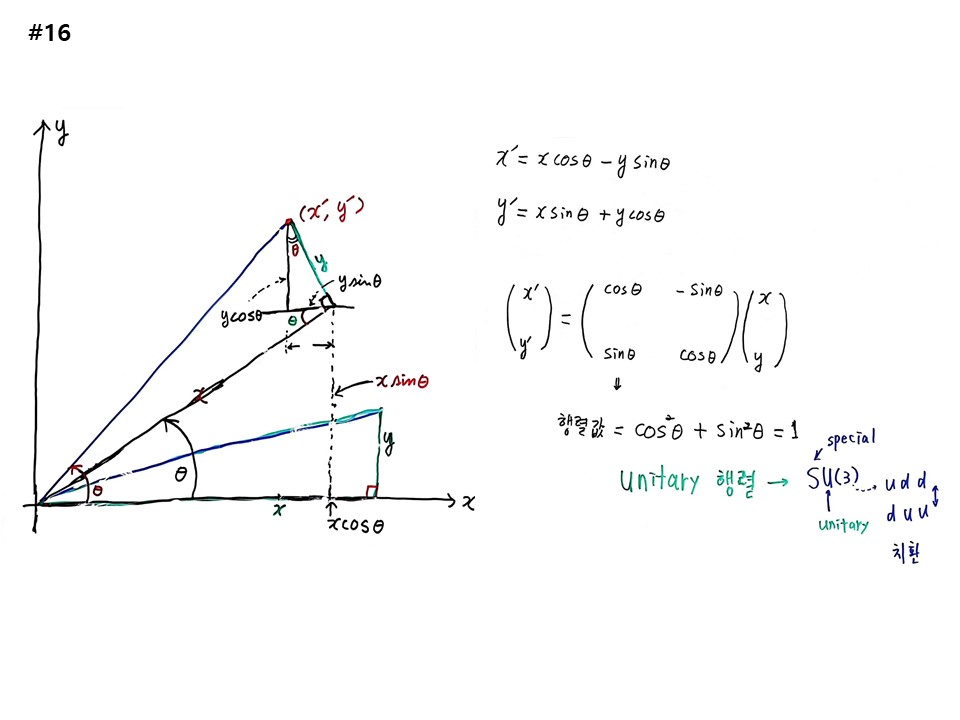
오늘은 회전이 행렬로 바뀐다는 것 까지 알고 가야 한다. 기하학의 좌표변환인데 회전이다. 양자역학은 회전이다. L 오퍼레이터는 각운동량으로 회전이다. 원자핵 주위에 전자가 회전하는 것이기 때문에 회전 오퍼레이터를 계산하는 것이 양자역학의 90%이다. 회전이 수학적으로 어떻다는 것을 알아야 이 상황을 알게 된다. 이것을 푸는 과정에 수학이나 물리학은 공부하는 것이 아니고 뚫어지게 보면 된다. 이해하는 것 하나도 없다. 이것이 익숙해져야 양자역학의 고금과정에 들어갈 수 있다.
도형을 크게 그린다. 직각삼각형 한 변이 x축에 있으면 수직으로 있는 꼭지점 좌표는 (x, y)가 되고 높이는 y이다. 직각삼각형을 원점에서 Θ 회전이동 시키면, (x’, y’)의 좌표를 구하는 문제이다. 회전이동한 삼각형을 하나 더 그려주면 보인다. 반지름을 그리면 더 헷갈린다.
x변이 Θ 움직이면 어디로 가는가? 회전시킨 삼각형의 직각에 x축 수평선을 그려주면 엇각으로 Θ를 알 수 있다. 또한 회전시킨 삼각형의 직각에서 X에 수직선을 그어주면, 그 길이는 xsinΘ가 된다. 또한 (x’,y’)과 만나는 수직선을 그려주면 꼭지점이 Θ이므로 높이는 ycosΘ가 된다. 회전시킨 삼각형의 직각에서 수직선이 x축과 만나는 점의 x길이는 xcosΘ가 되고, x축과 수평선을 그어 만들어진 작은 삼각형의 밑변길이는 ysinΘ가 된다.
따라서 x’=xcosΘ-ysinΘ, y’=xsinΘ+ycosΘ가 된다. 이것을 선형변환이라고 한다.
이것을 행렬로 바꾸면,
(x’ / y’) = ( cosΘ -sinΘ / sinΘ cosΘ)(x / y) 가 된다.
이 행렬의 행렬값(determinant)은 cos2Θ + sin2Θ =1 이다. 행렬값이 1인 행렬을 Unitary 행렬이라고 한다. SU에 U가 Unitary이다. 입자물리학의 모든 것을 Unitary 행렬로 설명한다는 것이다. 그래서 공간에서의 회전은 unitary 행렬로 표현이 된다는 것이다.
#17
갈루아의 연구를 조르당이 행렬로 표현했고, 나중에 리가 미분방정식으로 표현해서 무한소가 나와 물질, 에너지, 시간이 이 속에 다 설명이 된다. 그리고 마지막에 킬링이 SU로 분류를 했다. 이 모든 과정은 치환이다. 치환이라고 적고 대칭이라고 읽는다. 우리는 원자로 이루어진 것이 아니고 원자의 배열로 이루어졌다. 그 말은 나를 구성하는 원자는 원자의 배열인 구조는 놓아두고 한 달 만에 다 바뀐다. 피부세포는 하루만에 바뀐다.
대칭은 구조, 보존, 변환이다. 변환 하나를 회전이라는 것으로 보여 주었다. 변환인데 구조는 보존하라는 것이다. 변환하되 조건이 있다는 것이다. 그 조건이 주기율표를 만들고 우주를 만들고 인간을 만들었다. 눈물 날 정도이다. 그 조건 중 하나를 보여준 것이 주기율표를 만든 l값이다. 이것을 미분방정식의 경계치 조건이라고 한다. 경계에서 꽃이피고 우주가 출현했다. 입자물리학에서 가장 많이 나오는 변환이 연속변환이고, 연속변환이 원운동에서 나왔고, 연속변환은 무한소에 관한 변환이고, 무한소의 변환은 반드시 물질과 에너지와 시간을 불러온다. 그래서 우주를 설명하게 된다.
오늘 강의의 핵심은 여러분들이 다 기억해 보시고, 하나라도 이해하려고 하면 잘못된 것이다. 공부는 하는 것이 아니고 멈추는 것이다. 멈추었을 때 구조가 보이고, 구조는 그냥 받아 적으면 된다.

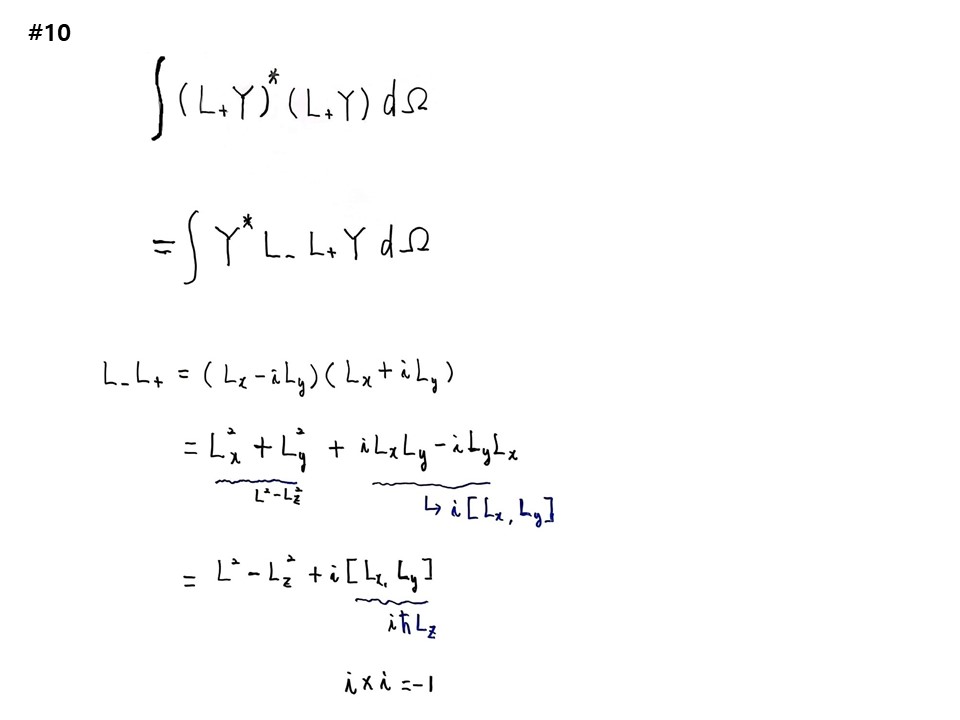
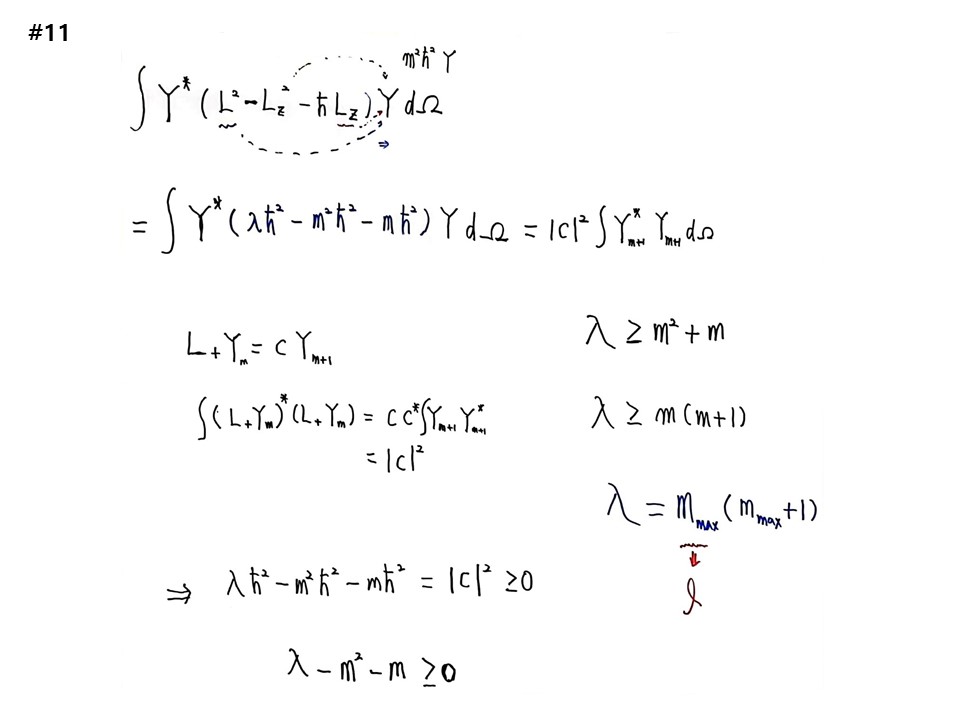
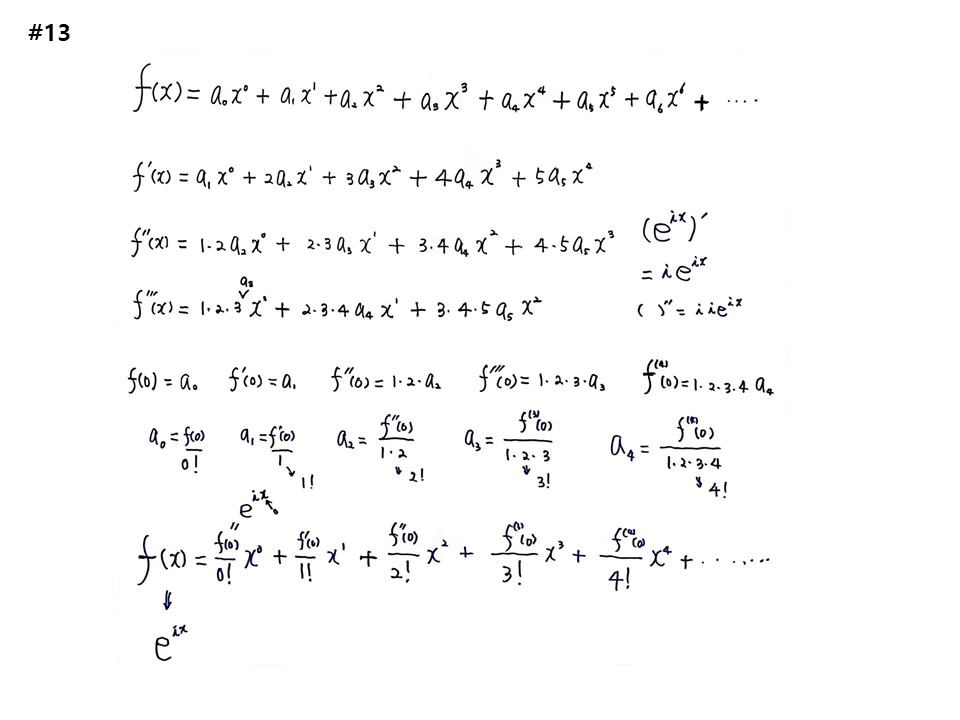
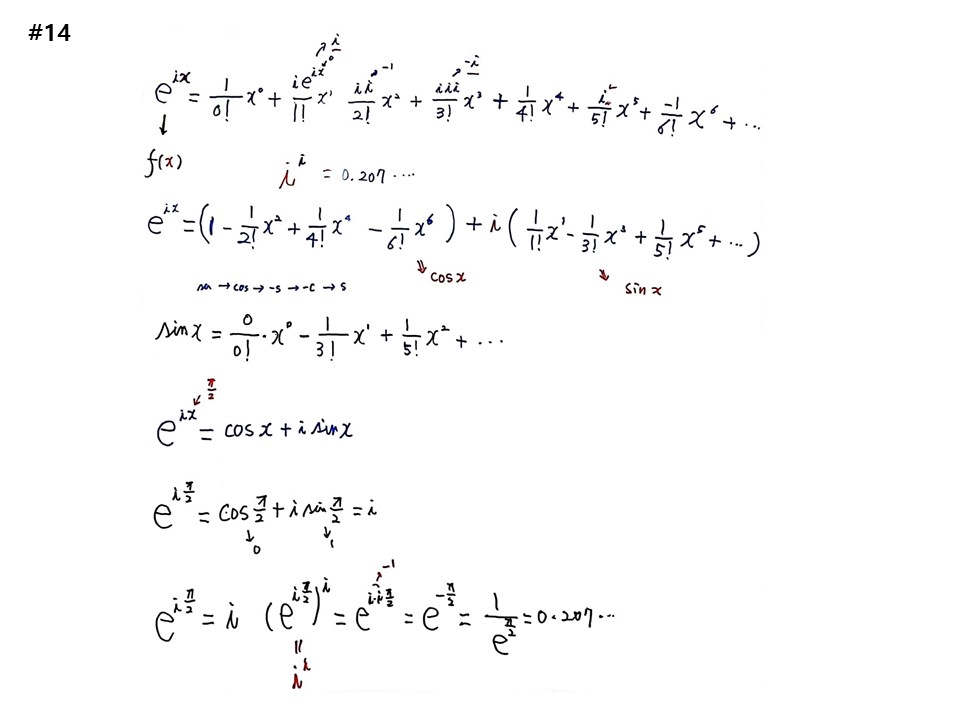
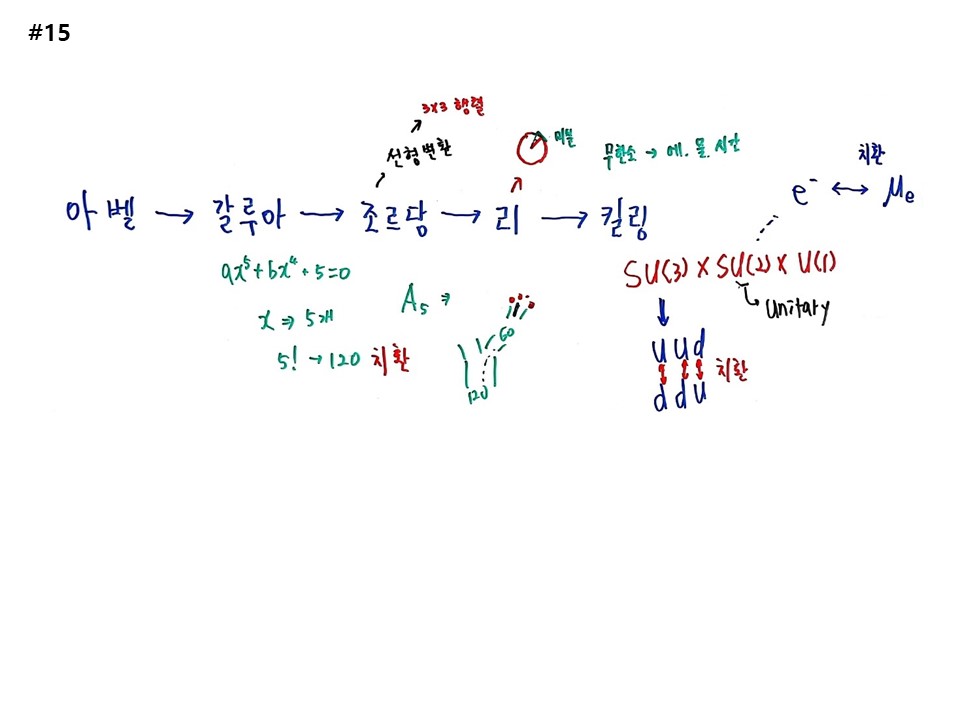

용량초과로 한번에 올라가지 않아 부득이하게 둘로 나누어 올리게 되었습니다.